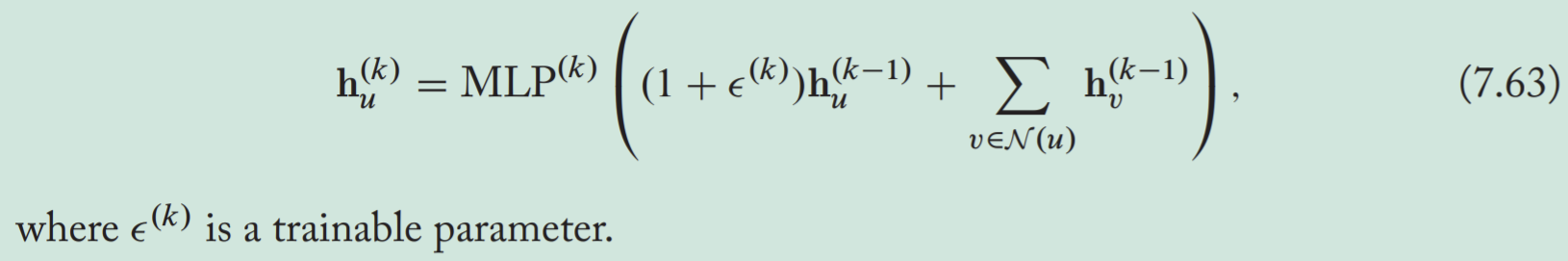Book-Graph Representation Learning

Book Graph Representation Learning

Chapter 1: Introduction

Graphs

• Types and represent edges
  • Simple graphs: at most one edge between each pair of nodes, no loop and undirected.
  • To represent graphs, adjacent matrix can be use. It shows as a symmetric matrix under simple graphs and may not symmetric under directed graphs.
  • Heterogeneous and multiplex graphs
    • Heterogeneous graphs: both nodes and graphs are heterogeneous.
    • Multiplex: graph can be decomposed in a set of \(k\) layers. Every layers corresponds to a unique relation, denoted as intra-layer edge, and those between layers are inter-layer edges. E.g., the graph of skeleton clips.
• Feature information
  • If heterogeneous, each types of nodes may have different dimensions of attributes.
• Tasks on graphs with machine learning
  • node classification: like whether users are bots or not, aka predict the label of node.
    • Note that the nodes in a graph are not independently and identically distributed, which doesn't satisfy the requirements of i.i.d. in supervised learning.
    • To inference the label, one idea is to use homophily, which assume that nodes tend to shared attributes with their neighbors in the graph. The other idea is structural equivalence, which assumes that nodes with similar local neighborhood structures will have similar labels.
  • Relation prediction
    • Like predicting the missing interactions.
    • Similar problems met in node classification (i.i.d.), and requires inductive biases that are specific to the graph domain.
  • Clustering and community detection
    • infer latent community structures given only the input graph.
  • Graph classification, regression and clustering.
    • In graph clustering, the goal is to learn an unsupervised measure of similarity between pairs of graphs.

Chapter 2: Background & Traditional Approaches

Graph statistics and kernel methods

Node-level statistics

• Node degree: simply counts the number of edges incident to a node, which will measure how many neighbors a node has.

• Node centrality: To measure the importance of a node in a graph.

  • Eigenvector centrality \(e_u\)

    • \(e_u=\frac{1}{\lambda}\sum\limits_{v\in V} \mathrm{A}[u,v]e_v,\forall u\in \mathcal{V}\)., it measures that satisfies the recurrence in above equation corresponds to an eigenvector of the adjacency matrix.

    • The vector of centrality values is given by the eigenvector corresponding to the largest eigenvalues of \(\mathrm{A}\).

    • The eigenvector centrality ranks the likelihood that a node is visited on a random walk of infinite length on the graph.

    • After \(t\) iteration, the eigenvector centrality will contain the number of length-\(t\) paths arriving at each node.

  • Betweeness centrality

    • Measures how often a node lies on the shortest path between two other nodes.

  • Closeness centrality

    • Measures the average shortest path length between a node and all other nodes.

  • More: M. Newman. Networks. Oxford University Press, 2018. 1, 12, 13, 108, 109

• The clustering coefficient

  • Measure the structural distinction using variations of the clustering coefficient, which Measures the proportion of closed triangles in a node's local neighborhood.

  • The local variant of clustering coefficient is calculated by:

    

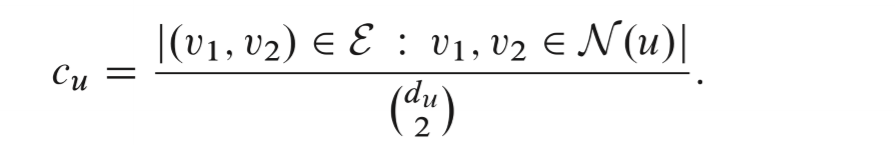
  • It Measures how tightly clustered a node's neighborhood is.

  • In social and biological sciences, they tend to have far higher clustering coefficients than one would expect if edges were sampled randomly.

• Closed Triangles, Ego Graphs, and Motifs

  • The global clustering coefficient. Similar equation but this time count in the node's ego graph.
  • A node's ego graph: the subgraph containing that node, its neighbors, and all the edges between nodes in its neighborhood.
  • The general version of these ideas is counting arbitrary motifs or graphlets within a node's ego graph. E.g.: triangles, cycles of particular length etc.

Graph-level features and graph kernels

• Bag of nodes

  • Aggregate node-level statistics
  • E.g., the histograms, the statistics based on the degrees, centralities and clustering coefficients of the nodes.
  • May miss important global properties in graph

• The Weisfieler-Lehman Kernel

  • Iterative neighborhood aggregation. Extract node-level features that contain more information than just their local Ego graph, and then to aggregate these features into a representation.

  • The most well-known one is the Weisfieler-Lehman (WL) algorithm.

    

    • In other words, the WL kernel is computed by measuring the difference between the resultant label sets for two graphs.
    • Useful while solving the isomorphism problem: approximate graph isomorphism is to check whether or not two graphs have the same label set after \(K\) rounds of the WL algorithm.

• Graphlets and path-base methods

  • Graphlets: count the occurrence of different small subgraph structures, but it's computationally difficult.
  • Path-based methods: examine the different kinds of paths that occur in the graph. E.g. random walk , the shortest path kernel that is similar as random walk but uses only the shortest-paths between nodes.

Neighborhood overlap detection

• The features mentioned above don't quantify the relationships among nodes, and thus won't work well on relation prediction.
• The simplest neighborhood overlap measure: just counts the number of neighbors that two nodes share.
• Hope that node-node similarity Measures computed on the training edges will lead to accurate predictions about the existence of test edges.

Local overlap measures

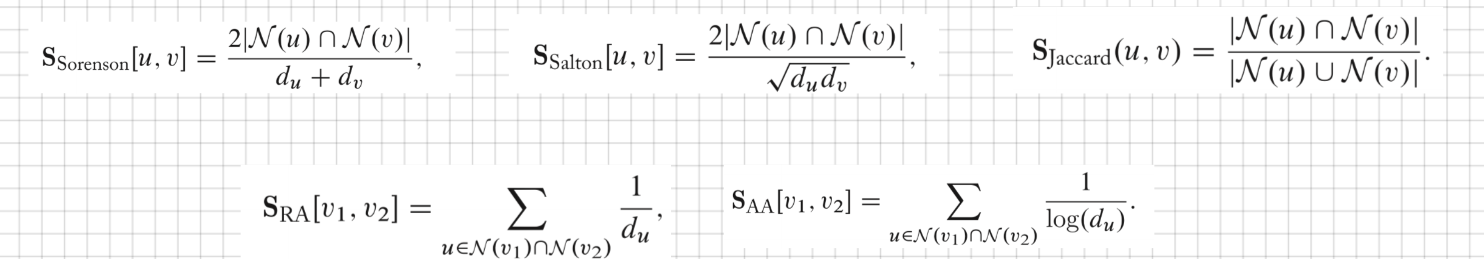
• Use the functions of the number of common neighbors two nodes share.
  • Sorensen index: normalized by the sum of the node degrees.
  • Salton index that normalizes by the product of the degrees of u and v.
  • Jaccard overlap: normalized by the degree of union u and v.
• Consider the importance of common neighbours, give more weight to common neighbours that have low degree.
  • Resource Allocation index (RA): counts the inverse degrees of the common neighbours.
  • Adamic-Adar index (AA): similar as RA but use the inverse logarithm of the degrees.

Global overlap measures

• Katz Index

  

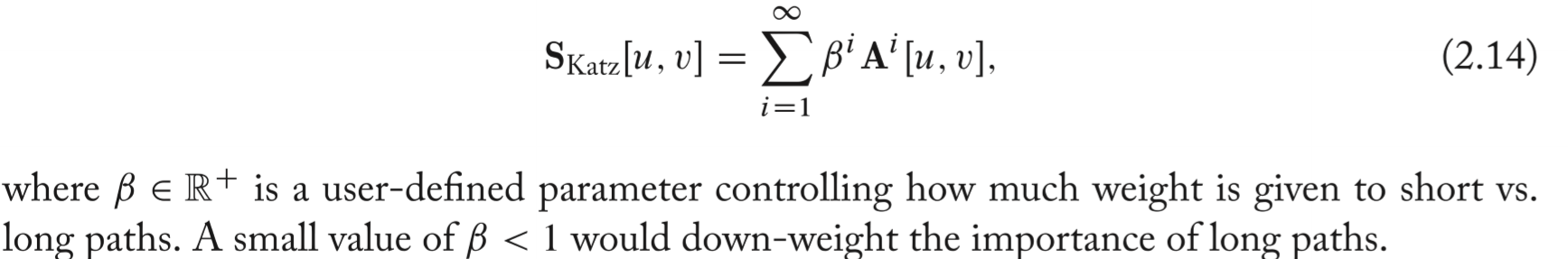
  • The most basic global overlap statistic. Simply count the number of paths of all lengths between a pair of nodes.
  • This index is a geometric series of matrices.
  • It's strongly biased by node degree which will give higher overall similarity scores when considering high-degree nodes cause they will generally be with more paths.

• Leicht, Holme, and Newman (LHN) similarity

  • Considering the ratio between the actual number of observed paths and the number of expected paths between two nodes.

  • To compute expectation, the configuration model is relied on. Under a random configuration model, the likelihood of an edge is simply proportional to the product of the two node degrees. But this heuristic calculation is intractable.

  • To approximate, the number of paths between two nodes grows by the largest eigenvalue of adjacent matrix. (The fact that the largest eigenvalue can be used to approximate the growth in the number of paths).

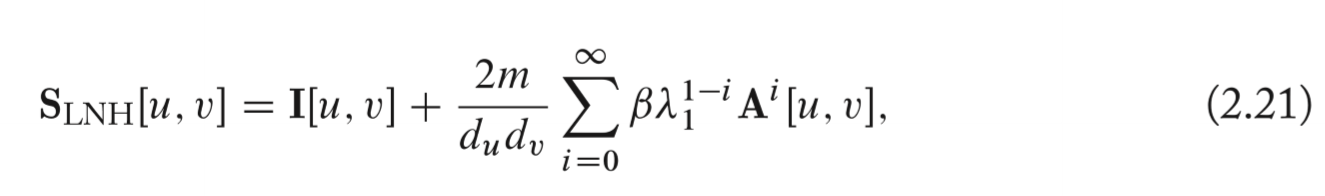    , and the solution to the matrix series can be written as \[ \mathrm{S_{LNH}}=2\alpha m\lambda_1 \mathrm{D^{-1}(I-\frac{\beta}{\lambda_1}A)^{-1}D^{-1}} \]

• Random walk methods

  • rather than exact count of paths over the graph in previous introduced index, consider random walks.
  • A measure of importance specific to node u will be obtained since the random walks are continually being teleported back to that node.
  • 

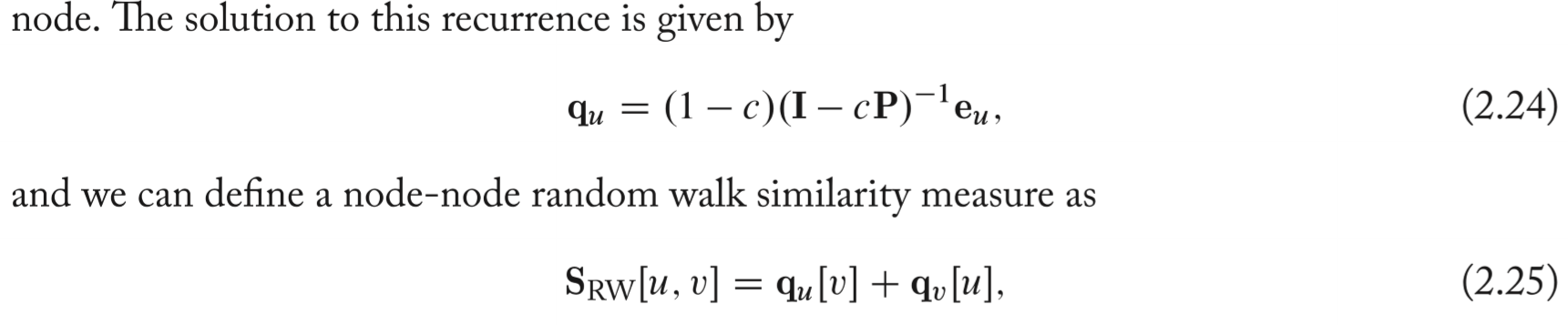
Graph Laplacians and spectral methods

learning to cluster the nodes in a graph.

Graph Laplacians

• Unnormalized Laplacian

  • \(\mathrm{L=D-A}\)

  • It's symmetric and positive semi-definite. \(\mathrm{L}\) has \(|V|\) non-negative eigenvalues.

  • \(\mathrm{x^TLx}=\sum\limits_{(u,v)\in\mathcal{E}}(\mathrm{x}[u]-\mathrm{x}[v])^2\)

  • If the graph contains \(K\) connected components, then there exists an ordering of the nodes in the graph such that the Laplacian matrix can be written as \[ \mathrm{L}={ \begin{bmatrix} \mathrm{L}_1 & & & \\ & \mathrm{L}_2 & & \\ & & \ddots& \\ & & & \mathrm{L}_K\\ \end{bmatrix} }, \] where each blocks is a valid graph Laplacian of a fully connected subgraph of the original graph. The spectrum of \(\mathrm{L}\) is the union of the eigenvalues of the \(\mathrm{L}_K\) matrices and the eigenvectors are the union of the eigenvectors of all the \(\mathrm{L}_K\) matrices with 0 values filled at the positions of the other blocks.

• Normalized Laplacians

  • \(\mathrm{L_{sym}=D^{-\frac{1}{2}}LD^{-\frac{1}{2}}}\), while random walk Laplacian is defined as \(\mathrm{L_{RW}=D^{-1}L}\).
  • For \(\mathrm{L_{sym}}\), the properties of previous mentioned holds but with the eigenvectors for the 0 eigenvalue scaled by \(\mathrm{D^{\frac{1}{2}}}\). For \(\mathrm{L_{RW}}\), the properties hold exactly.

• These methods just allow to cluster nodes that are already in disconnected components. The Laplacian can be used to get an optimal clustering of nodes within a fully connected graph.

Graph cuts and clustering

• Graph cuts

  • An optimal cluster means that a partition that minimizes the cut value, which is the count of how many edges cross the boundary between the partition of nodes. Theoretically the methods tend to simply make clusters that consists of a single node.
  • One way to solve this is minimizing the Ratio Cut, which penalizes the solution of choosing small cluster sizes.
  • Another popular solution is minimize the Normalized Cut (NCut), which enforces that all clusters have a similar number of edges incident to their a nodes.

• Approximating the RatioCut with the Laplacian Spectrum

  • The ratio cut minimization problem can be approximated as

    

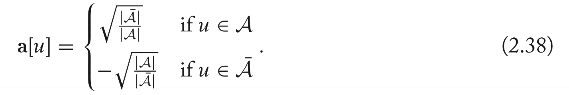
  • The formula above is NP-hard, after simplification, it will be :

    , and the solution of this problem is the second smallest eigenvector of \(\mathrm{L}\).

• Generalized spectral clustering

  • 

Part I: Node Embeddings

Chapter 3 Neighborhood Reconstruction Methods

Goal: encode nodes as low-dimensional vectors that summarize their graph position and the structure of their local graph neighborhood.

An encoder-decoder perspective

An encoder maps each node in the graph into a low-dimensional vector or embedding, a decoder takes the embeddings and uses them to reconstruct information about each node's neighborhood.

The encoder

• Most works rely on shallow embedding, where this encoder function is simply an embedding lookup based on the node ID.
• The generalized encoders are called GNNs.

The decoder

• They might predict the neighbors of one given node or one row in the graph adjacency matrix.
• The standard practice is to define pairwise decoders, which can be interpreted as predicting the relationship or similarity between pairs of nodes.
• While reconstruction, the goal is to optimize the encoder and decoder to minimize the reconstruction loss.

Optimizing an encoder-decoder model

• Usually use SGD, and minimize the disparity of decoded latent distance and real distance.

Typical encoder-decoder methods

Factorization-based approaches

Methods below are classified as factorization methods case their loss functions can be minimized using factorization algorithms like SVD.

The goal of these methods is to learn embeddings for each node such that the inner product between the learned embedding vectors approximates some deterministic measure of node similarity.

The inner product methods all employ deterministic measures of node similarity.

Laplacian eigenmaps (LE)

• Builds upon the spectral clustering

• Formula: \[ \mathcal{L}=\sum\limits_{(u,v)\in\mathcal{D}}\mathrm{DEC}(\mathrm{z}_u,\mathrm{z}_v)\cdot\mathrm{S}[u,v], \] which penalizes the model when very similar nodes have embeddings that are far apart.

• If the reconstructed \(\mathrm{S}\) satisfies the properties of a Laplacian matrix, then the node embeddings that minimize the loss are identical to the solution for a spectral clustering.

Inner-product methods

• More recent work employs inner-product, which assumes that the similarity between two nodes, e.g., the overlap between their local neighborhoods is proportional to the dot product of their embeddings.
• Examples:
  • Graph factorization: Distributed large-scale natural graph factorization
  • GraRep: Learning graph representations with global structural information
  • HOPE: Asymmetric transitivity preserving graph embedding
  • All of them used the mean squared error as loss function. They differ primarily in how they define \(\mathrm{S[u,v]}\). GF uses the adjacency matrix and sets \(\mathrm{S=A}\), GraRep defines \(\mathrm{S}\) based on powers of the adjacency matrix and HOPE supports general neighborhood overlap measures.

Random walk embedding

Use stochastic measures of node neighborhood overlap.

Deepwalk and node2vec

• The two methods differ on the inner-product decoder (the notions of node similarity and neighborhood reconstruction). They all optimize embeddings to encode the statistics of random walks. Mathematically, the goal is to learn embeddings so that \[ \mathrm{DEC(z}_u,\mathrm{z}_v)\triangleq\frac{\mathrm{z}_u^\top\mathrm{z}_v}{\sum\limits_{v_k\in\mathcal{V}}\mathrm{z}_u^\top\mathrm{z}_k}\approx p_{\mathcal{G,T}}(v|u),\label{4} \] where \(p_{\mathcal{G,T}}(v|u)\) is the probability of visiting \(v\) on a length-\(T\) random walk starting at \(u\), and \(T\) is the range.

• To train the random walk embeddings, use the cross-entropy loss.

• DeepWalk employs a hierarchical softmax to approximate equation above, where the normalizing factor is approximated using negative samples in the following way \[ \mathcal{L}=\sum\limits_{(u,v)\in\mathcal{D}}-\log(\sigma(\mathrm{z}_u^\top\mathrm{z}_v))-\gamma\mathbb{E}_{v_n\sim P_n{\mathcal{V}}}[\log(-\sigma(\mathrm{z}_u^\top\mathrm{z}_v))] \]

• DeepWalk employ uniformly random walks to define the visiting probability and node2vec use hyperparameters to allow the probabilities to smoothly interpolate between walks.

LINE

• Large-scale information network embeddings. Rather than explicitly leverage random walks, it shares ideas from DeepWalk and node2vec. It combines two encoder-decoder objectives.
• It has two objectives, the 1starting is \(\mathrm{DEC(z}_u,\mathrm{z}_v)=\frac{1}{1+e^{-\mathrm{z}_u^\top\mathrm{z}_v}}\), and the 2nd has the same equation as \[\eqref{4}\],but takes the KL-divergence to encode two-hop adjacency information.
• Instead of random walks, it explicitly reconstructs 1st and 2nd order neighborhood information.

Additional variants of the random-walk

• biasing or modifying the random walks.
  • consider random walks that skip over nodes, Perozzi et al.
  • define random walks based on the structural relationships between nodes: Ribeiro et al.

Random walk and matrix factorization

• https://dl.acm.org/doi/10.1145/3159652.3159706
• Random walk are closely related to matrix factorization.
• The embeddings learned by DeepWalk are closely related to the spectral clustering embeddings, but DeepWalk embeddings control the influence of different eigenvalues through T.
• The disadvantages of shallow embedding
  • It doesn't share any parameters between noes in the encoder, and therefore statistically and computationally inefficient.
  • It doesn't leverage node features in the encoder.
  • It's inherently trans-ductive, which means it only generate embeddings for nodes that were present during the training phase.

Chapter 4: Multi-relational data and knowledge graphs

The knowledge graph completion is to predict missing edges in the graph, generally. Below only covers the node embeddings way in graph completion.

Reconstruction multi-relational data

• Note the edges have multiple types, and the input for decoder will be a pair of nodes and types of the edge.

• One simple way is RESCAL: \[ \mathrm{DEC}(u,\tau,v)=\mathrm{z}_u^\top\,\mathrm{R}_\tau\mathrm{z}_v, \] where the embeddings \(\mathrm{z}\) and relation matrices \(\mathrm{R}\) are all learnable.

• While solving the Reconstruction error, it's like tensor factorization.

• Nearly all multi-relational embedding methods simply define the similarity measure directly based on the adjacency tensor, or to say they all try to reconstruct immediate neighbors from the low-dimensional embeddings.

Loss functions

Cross-entropy with negative sampling

• The formula

\[ \mathcal{L}=\sum\limits_{(u,\tau,v)\in\mathcal{E}}-\log(\sigma(\mathrm{DEC(z}_u,\tau,\mathrm{z}_v)))-\gamma\mathbb{E}_{v_n\sim P_{n,u}{\mathcal{V}}}[\log(\sigma(-\mathrm{DEC(z}_u,\tau,\mathrm{z}_{v_n}))], \]

where \(P_{n,u}(\mathcal{V})\) denotes a negative sampling distribution. The 1st term denotes the log-likelihood that we predict "true" for an edge that does actually exist in the graph, and the 2nd term is the expected log-likelihood that is correctly predicted "false" for an edge that does not exist in the graph.

After approximating with Monte Carlo, the loss will be \[ \mathcal{L}=\sum\limits_{(u,\tau,v)\in\mathcal{E}}-\log(\sigma(\mathrm{DEC(z}_u,\tau,\mathrm{z}_v)))-\sum\limits_{v_n\in \mathcal{P}_{n,u}}[\log(\sigma(-\mathrm{DEC(z}_u,\tau,\mathrm{z}_{v_n}))], \] , where \(\mathcal{P}_{n,u}\) is a set of nodes sampled from \(P_{n,u}(\mathcal{V})\).

• How to define negative sampling distribution?
  • Simply use a uniform distribution over all nodes, but this may get false negative.
  • Sample negative samples that satisfy a predefined type constraints.
  • Draw negative samples for both the head node and the tail node of the relation.

Max-Margin loss

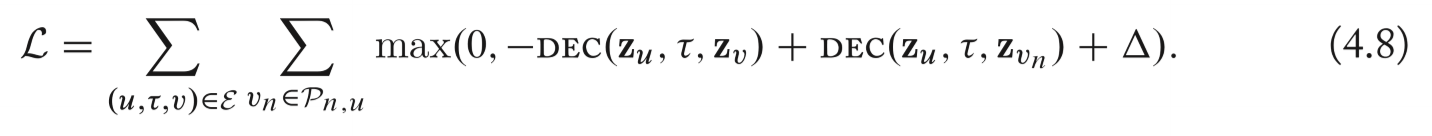
Contrastive estimation to get the negative sample.

Multi-relational decoders

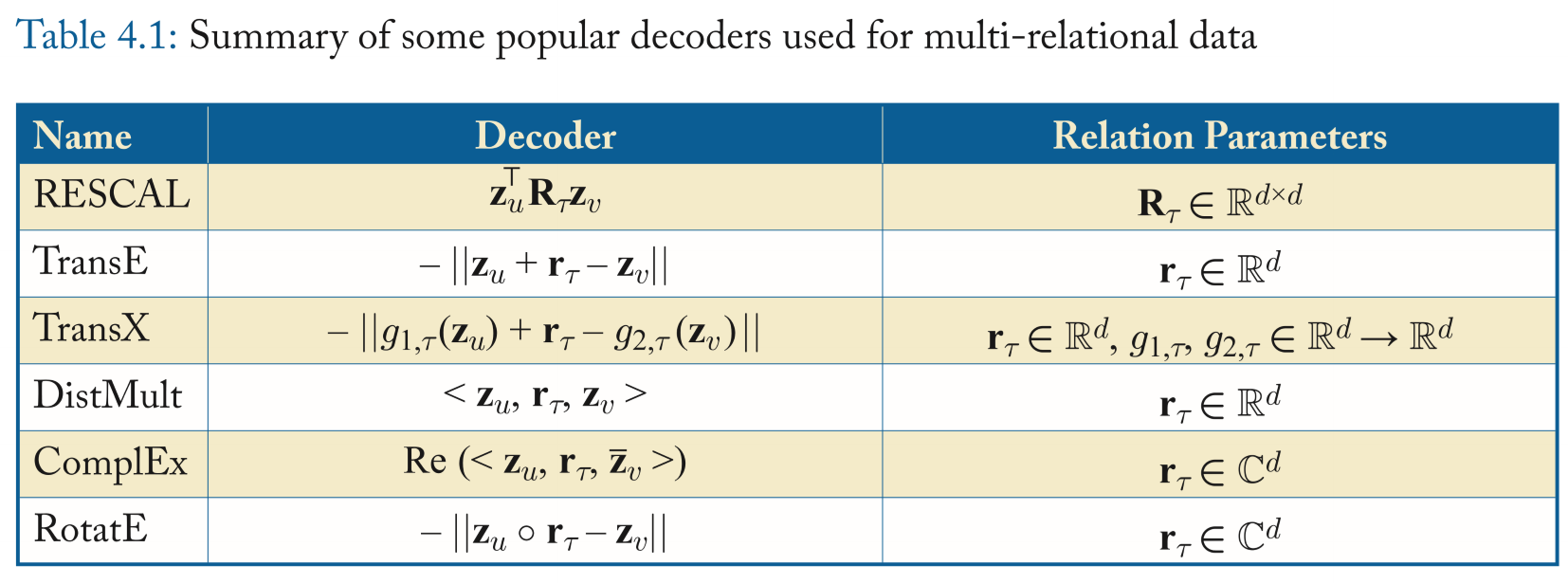
Methods

• RESCAL

But it's computationally expensive.

• Translational Decoders

  • TransE, the likelihood of an edge is proportional to the distance between the embedding of the head node and the tail node, after translating the head node according to the relation embedding. \[ \mathrm{DEC(z}_u,\tau,\mathrm{z}_{v})=-\|\mathrm{z}_u+\mathrm{r}_\tau-\mathrm{z}_{v}\| \]

  • Limitation: simplicity.

  • The variants of TransE

    • TransX

      Import a trainable transformation that depend on the relation \(\tau\). \[ \mathrm{DEC(z}_u,\tau,\mathrm{z}_{v})=-\|g_{1,\tau}(\mathrm{z}_u)+\mathrm{r}_\tau-g_{2,\tau}(\mathrm{z}_{v})\| \]

    • TransH

      Project the entity embeddings onto a learnable relation-specific hyperplane-defined by the normal vector \(\mathrm{w}_r\)-before performing translation.

• Multi-Liner dot products
  • Also known as DistMult.
  • 
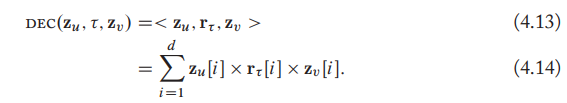
  • Generalizing the dot-product decoder from simple graphs.
  • One limitation is that it can only encode symmetric relations while there are many directed graph and thus they are asymmetric.
• Complex decoders

  • ComplEx, augmenting the DistMult by employing complex-valued embeddings. It's defined as

    

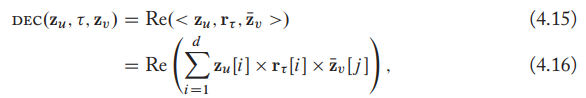
  • RotatE defies the decoder as rotations in the complex plane as:

    

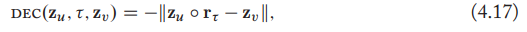
    each dimension of the relation embedding can be represented as \(\mathrm{r}_\tau[i]=e^{i\theta_{r,i}}\) and thus corresponds to a rotation in the complex plane.

Representational abilities

The Multi-relational decoders can represent different logical patterns on relations.

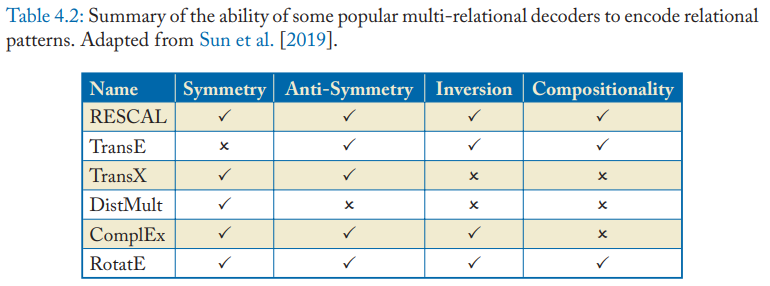
• Symmetry and anti-symmetry
  • Symmetric decoders: DistMult
  • Anti-symmetric decoders: TransE
• Inversion: implies the existence of another with opposite directionality.
• Compositionality:
  • RESCAL: \(\mathrm{R_{\tau_3}=R_{\tau_2}R_{\tau_1}}\)
  • TransE: \(\mathrm{r_{\tau_3}=r_{\tau_2}+r_{\tau_1}}\)

Part II: GNNs

Chapter 5 The GNN model

GNNs are more complex than shallow embedding, they will generate representations of nodes that actually depend on the structure of the graph.

A key desideratum of GNNs is that they should be permutation invariant.

Neural message passing

After GNN, the embeddings contain structure-based information and feature-based information. However, the feature based information is in their k-hop neighborhoods.

The message passing in GNN can be taken as using update and aggregate functions.

The basic GNN

• The message passing in basic GNN framework is like a standard multi-layer perception.

With self-loop

• Add self-loops to omit the explicit update step.
• This can alleviate overfitting, but also limit the expressivity of the GNN, sample the information coming the nodes neighbours cannot be differentiated from the information from the node itself.
• In basic GNN, adding self-loops means sharing parameters between the \(\mathrm{W}_{self}\) and \(\mathrm{W}_{neigh}\) matrices.

Generalized neighborhood aggregation

Neighborhood normalization

• Simply normalized the aggregation operation based upon the degrees of the nodes involved:

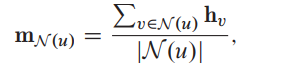
• Symmetric normalization:

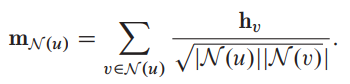
• Combining the symmetric-normalized aggregation along with the basic GNNs update function results in a first-order approximation of a spectral graph convolution.

• GCNs

  • They use symmetric-normalized aggregation as well as the self-loop update approach.

    

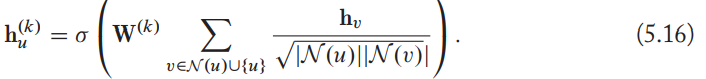
  • In GNN, the use of normalization can lead to a loss of information.

  • Normalization is most helpful in tasks where noes feature information is far more useful than structural information, or where there is a very wide range of node degrees that can lead to instabilities during optimization.

Set aggregation

The embeddings of neighbours, there is no natural ordering of a nodes' neighbours, and any aggregation function we define must thus be permutation invariant.

• Set pooling

  • Define an aggregation function based on permutation invariant, can be implemented by just adding some MLP layers, e.g.

    

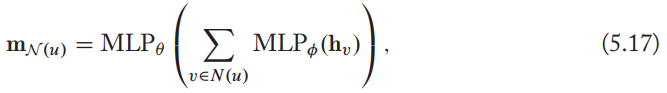
    this always lead to small increases in performance, though with the risk of overfitting.

  • Or use element-wise maximum or minimum to replace summation.

• Janossy pooling

  • More powerful, apply a permutation-sensitive function and average the result over many possible permutations. In practice, the permutation-sensitive function is defined to be an LSTM.

    

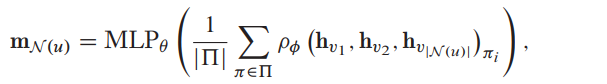
  • If the set of permutations \(\prod\) is equal to all possible permutations, then the aggregator is also a universal function approximator for sets. Like simple summation based set pooling.

  • In practice, Janossy pooling employs one of two approaches

    • Sample a random subsets of possible permutations during each application of the aggregator, and only sum over that random subset.
    • Employ a canonical ordering of the nodes in the neighborhood set, e.g., order the nodes in descending order according to their degree, with ties broken randomly.

  • Janossy-style pooling can improve upon set pooling in a number of synthetic evaluation setups.

Neighborhood attention

• Assign an attention weight or importance to each neighbour, which is used to weigh this neighbor's influence during the aggregation step.

  

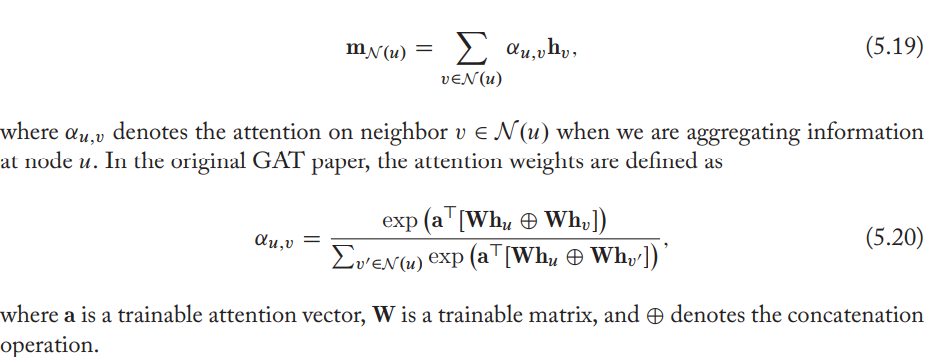
• Popular variants of attention include the bilinear attention model and variations of attention layers using MLPs.

• Multi heads methods are popular, which is also known as transformer.

  • The basic idea behind transformers is to define neural network layers entirely based n the attention operation. The basic transformer layer is extractly equivalent to a GNNs layer using multi-headed attention if we assume that the GNNs receives a fully connected graph input.
  • The time complexity is the square of the number of nodes cause each pairs attention need to be calculated.
  • Attention can influence the inductive bias of GNNs.

Generalized update methods

• One popular way is GraphSAGE, which introduced the idea of generalized Neighborhood aggregation.

• Over-smoothing of GNN: after several iterations of GNN message passing, the representations for all the nodes in the graph can become very similar to one another.

  

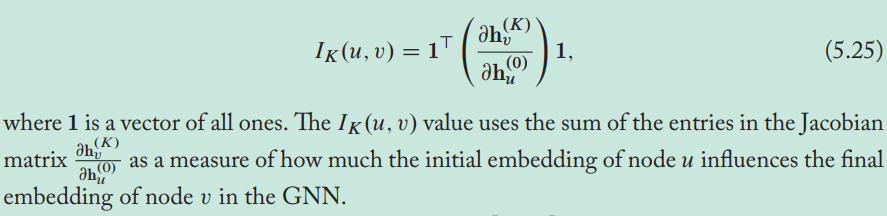
• The measure of how much the initial embedding of node \(u\) influences the final embedding of node \(v\) in the GNN is proportional to the probability of visiting node \(v\) on a length-\(k\) random walk starting from node \(u\).

As \(k\rightarrow\infin\), the influence of every node approaches the stationary distribution of random walks over the graph, meaning that local neighborhood information is lost.

• When using simple GNN models, and especially those with the self-loop update approach-building deeper models can actually hurt performance.

Concatenation and skip-connections

Like using vector concatenation or skip connection that try to directly preserve information from previous rounds of message passing during the update step.

• Do concatenation to preserve more node-level information during message passing
  • The key intuition is that we encourage the model to disentangle information during message passing--separating the information coming from the neighbors from the current representation of each model.
• Do linear interpolation between the previous representation and the representation that was updated based on the neighborhood information.
• In practice, these techniques tend to be most useful for node classification tasks with moderately deep GNNs, and excel on tasks that exhibit homophily.

Gated updates

One way to view the GNN meaning passing is that the aggregation function is receiving an observation from the neighbors, which is then used to update the hidden state of each node. Simply replace the hidden state argument of the RNN update function with the node's hidden state, and replace the observation vector with the message aggregated from the local neighborhood.

• GRU based
• LSTM based

Jumping knowledge connection

To improve the quality of the final node representations

• Jumping knowledge connections: One simple way is to simply leverage the representations at each layer of message passing, rather than only using the final layer output.
• With max-pooling and LSTM attention layers the result is improved.

Edge features and Multi-relational GNNs

Relational GNNs

• RGCN: relational graph convolutional network

  

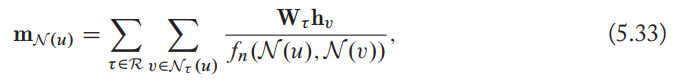
  • Augment the aggregation function to accommodate multiple relation types by specifying a separate transformation matrix per relation type.
  • The Multi-relational aggregation in RGCN is thus analogous to the basic a GNN approach with normalization, but we separately aggregate information across different edge types.

• Parameter sharing

  • For RGCN, the increase of number of parameters is caused by that each edge type requires a trainable matrix.

  • To fix this, Schlichtkrull et al. proposed to share with basis matrices, aka an alternative view of the parameter sharing RGCN approach is that we are learning an embedding for each relation, as well as a tensor that is shared across all relations.

    

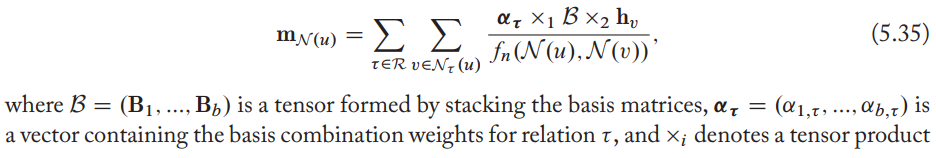
• Extensions and variations

  • define separate aggregation matrices per relation as relational GNNs.
    • without parameter sharing
    • http://dx.doi.org/10.18653/v1/d17-1159
    • RGCN+attention

Attention and feature concatenation

https://www.aclweb.org/anthology/D19-1458/

Graph pooling

To get representations in graph-level cause the goal is to pool together the node embedding in order to learn an embedding of the entire graph.

• Set pooling approaches

  • One popular way it taking a sum or mean of the node embeddings. This is sufficient for small graphs.
  • The other popular way is using a combination of LSTM and attention to pool the node embeddings.
    • The way is like what's done is one-head bert, the output of graph-level representation is the concatenation of output from different timestep.

• Graph coarsening approaches

  To exploit the structure of the graph. One popular strategy to accomplish this is to perform graph clustering or coarseing as a means to pool the node representations.

  • Estimate assignment matrices
    • Use spectral clustering (the decomposition of adjacent matrix to estimate assignment matrix (from node representations to graph-level representations.))
    • Employ another GNN to predict cluster assignments
  • Use the assignment matrices to coarsen the graph.

Generalized message passing

Leverage edge and graph-level information at each stage of message passing

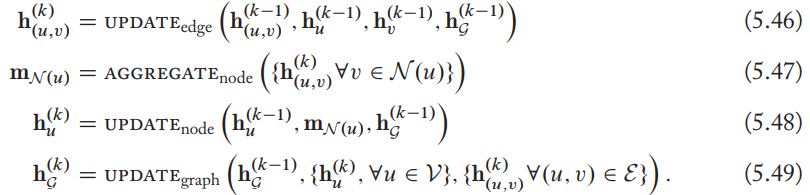
Chapter 6 GNNs in practice

optimization, regularization and application-based

Applications and loss functions

• GNNs for node classification

  • If fully supervised, use the negative log-likelihood loss and softmax to denote the predicted probability.
  • transductive and inductive nodes
    • transductive nodes: nodes used while training but not covered while calculating loss. Semi-supervised means that the GNN is tested on transductive nodes.
    • inductive: not used in either the loss computation or the GNN message passing operations during training.

• GNNs for graph classification

  • similar loss functions but use graph-level representations.

• GNNs for relation prediction

  • use the pairwise node embedding loss functions.

• Pretraining

  • Pre-training the GNN using one of the neighborhood reconstruction losses.

    • E.g., pre-train a GNN to reconstruct missing edges in the graph before fine-tuning on a node classification loss. However, Veličković et al found that a randomly initialized GNN is equally strong compared to one pre-trained on a neighborhood reconstruction loss.

    • DGI (deep graph infomax): maximize the mutual information between node embeddings and graph embeddings. The basic idea is the GNN model must learn to generate node embeddings that can distinguish between the real graph and its corrupted counterpart.

      

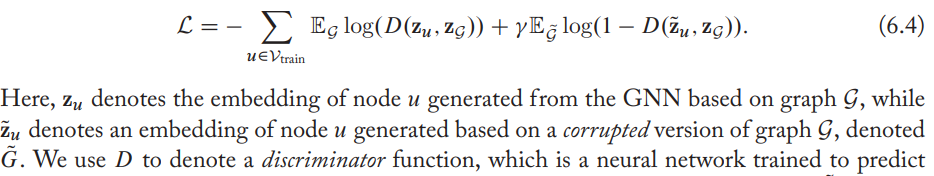
Efficiency concerns and node sampling

• Graph-level implementations

  • Use sparse matrix multiplications and add self-loops to avoid redundant computations, but it requires operating on tested entire graph and all node features simultaneously, which may not be feasible due to memory limitations.

• Sampling and mini-batch

  Work with a subset of nodes during message passing.

  • The challenge is we cannot simply Run message passing on a subsets of the nodes in a graph without losing information.
  • One way is subsampling node neighbors. First select a set of target nodes for a batch and then to recursively sample the neighbors of these nodes in order to ensure that the connectivity of the graph is maintained. Subsample the neighbors of each node, using a fixed sample size to improve the efficiency of batched tensor operations.

Parameter sharing and regularization

Like L2 regularization, dropout and layer normalization that both work on GNNs and CNNs.

• Parameter sharing across layers
  • use the same parameters in all the aggregate and update functions in the GNN. It's most effective in GNNs with more than six layers, and is often used in conjunction with gated update functions.
• Edge dropout
  • randomly remove edges in the adjacency matrix during training, with the intuition that this will make the GNN less prone to overfitting and more robust to noise in the adjacency matrix.
  • The neighborhood subsampling approaches lead to this kind of regularization as a side effect, making it a very common strategy in large-scale GNN applications.

Chapter 7 Theoretical motivations

GNNs and graph convolutions

Generalize the notion of convolutions to general graph structured data.

Convolutions and the Fourier transform

• The Fourier analysis
  • The coefficients of Fourier series tell the amplitude if the complex sinusoidal component \(e^{-\frac{i2\pi}{N}k}\).
  • The high-frequency components have a large \(k\) and vary quickly while the low-frequency components have small \(k\) and vary more slowly.
• Translation equivalent: translating a signal and then convolving it by a filter is equivalent to convolving the signal and then translating the result.

From time signals to graph signals

• Each point in time \(t\) is represented as a node and the edges in graph thus represent how the signal propagates
• Represent operations such as time-shifts using the adjacency and Laplacian matrices of the graph.
• Multiplying a signal by the adjacency matrix propagates signals from node to node, and multiplication by the Laplacian computes the difference between a signal at each node and its immediate neighbors.
• shifts and convolutions on time-varying discrete signals can be represented based on the adjacency matrix and Laplacian matrix of a chain graph.
• The convolution operation matrix satisfies translation equivalence.
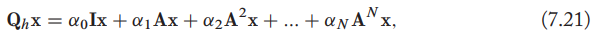• , which means that the convolved signal \(\mathrm{Q_hx}[u]\) at each node \(u\in\mathcal{V}\) will correspond to some mixture of the information in the node's \(N\)-hop neighborhood, with the \(\alpha_0,\alpha_1,\cdots,\alpha_N\) controlling the strength of the information coming from different hops. Defining \(\mathrm{Q_h}\) in this way guarantees that our filter commutes with the adjacency matrix, satisfying a generalized notion of translation equivariance.
• By stacking multiple message passing layers, GNNs are able to implicitly operate on higher-order polynomials of the adjacency matrix.
• The symmetric normalized Laplacian or symmetric normalized adjacency matrix are usually taken as the convolutional filters cause
  • They have bounded spectrums and thus numerically stable.
  • They are simultaneously diagonalizable, which means that they share the same eigenvectors.

Spectral graph convolutions

• 

  The Laplace operator (\(\Delta\)) tells us the average difference between the function value at a point and function values in the neighboring regions surrounding this point. The Laplacian matrix is regarded as a discrete analog of the Laplace operator since it allows to quantity the difference between the value at a node and the values at that node's neighbors.

• The eigenfunctions of Laplace operator is corresponds to the complex exponentials, which means the eigenfunctions of \(-\Delta e^{2\pi ist}\) are the same complex exponentials that make up the modes of the frequency domain in the Fourier transform, with the corresponding eigenvalue indicating the frequency.

• Graph convolution can be represented as polynomials of the Laplacian (or one of its normalized variants).

• Given the graph Fourier coefficients \(\mathrm{U^\top f}\) of a signal \(\mathrm{f}\) as well as the graph Fourier coefficients \(\mathrm{U^\top h}\) of some filter \(\mathrm{h}\), we can compute a graph convolution via element-wise products as \[ \mathrm{f\star_\mathcal{G}h=U(U^\top f \circ U^\top h)} \] Then represent convolutions in the spectral domain based on the graph Fourier coefficients \(\theta_h=\mathrm{U^\top h \in \mathbb{R}^{|\mathcal{V}|}}\).

• One way is to learn a nonparametric filter by directly optimizing \(\theta_h\) (spectral filter) and defining the convolution as \(\mathrm{f\star_\mathcal{G}h=U(U^\top f \circ }\theta_h)=(\mathrm{Udiag}(\theta_h)\mathrm{U}^\top)\mathrm{f}\). But this way has no real dependency on the structure of the graph and may not satisfy many of the properties that we want from a convolution, e.g. locality.

• To make sure the spectral filter \(\theta_h\) is corresponds to a meaningful convolution on the graph, another way is to parameterize \(\theta_h\) based on the eigenvalues of the Laplacian, e.g., a degree \(N\) polynomial of the eigenvalues of the Laplacian and thus ensure the filtered signal at each node depends on information in its \(k\)-hop neighborhood.

  \(\mathrm{f\star_\mathcal{G}h}=(\mathrm{Up_N}(\Lambda)\mathrm{U}^\top)\mathrm{f}=p_N(\mathrm{L})\mathrm{f}\).

• The filter (e.g., Fourier) coefficients cannot be simply interpreted as corresponding to different frequencies.

  • 
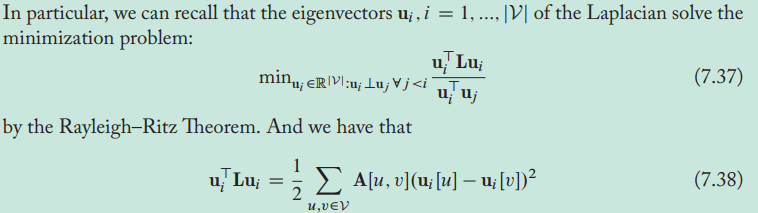
  • The smallest eigenvector of the Laplacian corresponds to a signal that varies from node to node by the least amount on the graph, the second-smallest eigenvector corresponds to a signal that varies the second smallest amount and so on.
  • Laplacian eigenvectors can be used to assign nodes to communities so that we minimize the number of edges that go between communities. The Laplacian eigenvectors define signals that vary in a smooth way across the graph, with the smoothest signals indicating the coarse-gained community structure of the graph.

Convolution inspired GNNs

• Purely convolutional approaches

  • Directly optimize \(\theta_h\) or parameterize it
  • Methods
    • Bruna et al. : Nonparametric spectral filter and parametric spectral filter by a cubic spline.
    • Defferrard et al., parameterize the spectral filter by Chebyshev polynomials. Chebyshev polynomials have an efficient recursive formulation and have various properties that make them suitable for polynomial approximation.
    • Liao et al.,: learn polynomials of the Laplacian based on the Lanczos algorithm.
    • Beyond real-valued polynomials of the Laplacian (or the adjacency matrix): employ more general parametric rational complex functions of the Laplacian.
      • Levie et al.: Cayley polynomials of the Laplacian
      • Bianchi et al: ARMA filters.

• GCNs and connections to message passing

  • A basic GCN layer is defined as \[ \mathrm{H}^{(k)}=\sigma (\tilde{\mathrm{A}}\mathrm{H}^{(k-1)}\mathrm{W}^{(k)}),\\ \tilde{\mathrm{A}}=\mathrm{(D+I)^{-\frac{1}{2}}(I+A)(D+I)^{-\frac{1}{2}}}, \] where \(\mathrm{W}^{(k)}\) is a learnable parameter matrix. The model was initially motivated as a combination of a simple graph convolution (based on the polynomial \(\mathrm{I+A}\)), with a learnable weight matrix and a nonlinearity.

  • The notion of message passing can be viewed as corresponding to a simple form of graph convolutions combined with additional trainable weights and nonlinearites.

  • Stacking multiple rounds of message passing in a basic GNN is analogous to applying a low-pass convolutional filter, which produces a smoothed version of the input signal on the graph.

    • The multiplication \(\mathrm{A}^K_{sym}\mathrm{X}\) of the input node features by a high power of the adjacency matrix can be interpreted as convolutional filter based on the lowest-frequency signals of the graph Laplacian. Because multiplying a signal by high powers of \(\mathrm{A_{sym}}\) corresponds to a convolutional filter based on the lowest eigenvalues of \(\mathrm{L_{sym}}\), i.e., it produces a low-pass filter.
    • The deeper, the convolution filters are simpler.

• GNNs without message passing

  • Simplify GNNs by removing the iterative message passing process. The models are generally defined as \[ \mathrm{Z=MLP}_\theta(f(\mathrm{A)MLP_\phi(\mathrm{A})}) \]

    • Wu et al. define \(f(\mathrm{A})=\mathrm{\tilde{A}}^k\), with \(\tilde{\mathrm{A}}\) is the symmetric normalized adjacency matrix.

    • Klicpera et al. defines \(f\) by analogy to the personalized PageRank algorithm as \[ f(\mathrm{A})=\alpha(\mathrm{I-(1-\alpha)\tilde{A}})^{-1}=\alpha\sum\limits_{k=0}^{\infin}(\mathrm{I-\alpha\tilde{A}})^k, \] cause we often do not need to interleave trainable neural networks with graph convolution layers. We can simply use neural networks to learn feature transformations at the beginning and end of the model and apply a deterministic convolution layer to leverage the graph structure. Like GAT.

  • Using the symmetric normalized adjacency matrix with self-loops leads to effective graph convolutions.

    • Wu et al. proves that adding self-loops shrinks the spectrum of corresponding graph Laplacian by reducing the magnitude of the dominant eigenvalue.
    • Intuitively, adding self-loops decrease the influence of far-away noes and makes the filtered signal more dependent on local neighborhoods on the graph.

GNNs and probabilistic graphical models

View the embeddings for each node as latent variables that are inferred.

Hilbert space embeddings of distributions

• The density \(p(\mathrm{x})\) based on its expected value under the feature map \(\phi\) is: \[ \mu_\mathrm{x}=\int_{\mathbb{R}^m}\phi(\mathrm{x})p(\mathrm{x})d\mathrm{x} \] The formula will be injective under the assumption of Hilbert space embeddings of distributions. Then \(\mu_\mathrm{x}\) can serve as a sufficient statistics for \(p(\mathrm{x})\). Then any computations we want to perform on \(p(\mathrm{x})\) can be equivalently represented as functions of the embedding \(\mu_\mathrm{x}\). One well-known feature map \(\phi\) is Gaussian radial basis function.

• In the context of the connection to GNNs, the takeaway is simply that we can represent distributions \(p(\mathrm{x})\) as embeddings \(\mu_\mathrm{x}\) in some feature space.

Graphs as graphical models

• The notion of dependence between nodes is viewed as a formal, probabilistic way.

• Assume that a graph defines a Markov random field,

  

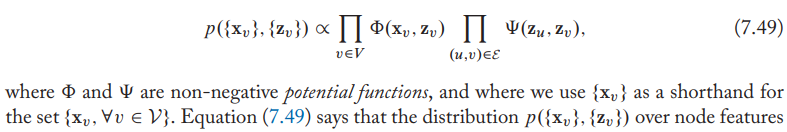
  • Intuitively, \(\Phi(\mathrm{x}_v,\mathrm{z}_v)\) indicates the likelihood of a node feature vector \(\mathrm{x}_v\) given its latent node embedding \(\mathrm{z}_v\), while \(\Psi\) controls the dependency between connected nodes.
  • Assume that node features are determined by their latent embeddings, and the latent embeddings for connected nodes are dependent on each other.

• GNNs will try to seek to implicitly learn the \(\Psi,\Phi\) by leveraging the Hilbert space embedding idea.

Embedding mean-field inference

The goal is to infer latent representations for all the nodes in the graph that can explain the dependencies between the observed node features.

• The key step is computing the posterior \(p(\{\mathrm{z}_v\}|\{\mathrm{x}_v\})\), i.e., computing the likelihood of a particular set of latent embeddings given the observed features. But the accurate solution is intractable, one way is to approximate it.

• One way to approximate the posterior is to employ mean-field variational inference, by which the posterior is approximated as \(p(\{\mathrm{z}_v\}|\{\mathrm{x}_v\})\approx q(\{\mathrm{z}_v\})=\prod\limits_{v\in\mathcal{V}}q_v(\mathrm{z}_v)\). The key intuition in mean-field inference is that we assume that the posterior distribution over the latent variables factorizes into \(\mathcal{V}\) independent distributions, one per node.

  • The standard approach to solve is to minimize the KL divergence between the approximate posterior and the true posterior. But directly minimize it is impossible cause evaluating the KL divergence requires knowledge of the true posterior.

    

    • To minimize the KL divergence easily, one way is to use the techniques from variational inference.
    • 
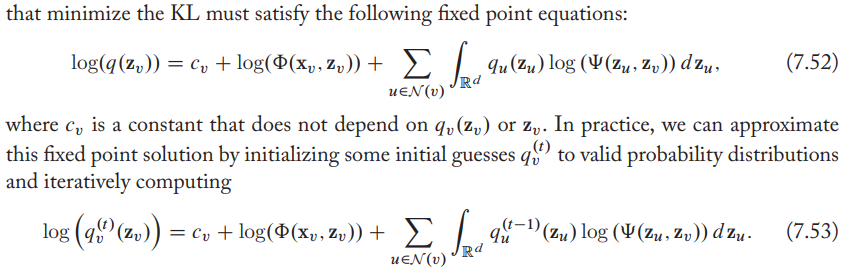
    • The approximate posterior at timestep \(t\) for each latent node embedding is a function of the node's feature \(\mathrm{z}_x\) and the marginal distributions (marginalized on the node's neighbors.) at previous timestep. Therefore, using variational inference to infer the posterior is really like message passing.
    • The key distinction is that the mean-field message passing equations operate over distributions rather than embeddings (what used in GNN).

• Another way is try to learn embeddings in an end-to-end way, or to say rather than specifying a concrete probabilistic model, one can simply learn embeddings that could correspond to some probabilistic model.

  • Dai et al. define \(f\) in an analogous manner to a basic GNN and thus at each iteration the updated Hilbert space embedding for node \(v\) is a function of its neighbors' embedding as well as its feature inputs.

GNNs and PGMs more generality

• Different variants of message passing can be derived based on different approximate inference algorithms. Dai et al.
• How GNNs can be integrated more generally into PGM models.
  • Qu et al.
  • Zhang et al.

GNNs and graph isomorphism

The motivation of GNNs based on connections to graph isomorphism testing.

Graph isomorphism and representational capacity

• Graph isomorphism
  • The goal of graph isomorphism is to declare whether or not the given two graphs are isomorphic. If so, the graphs are essentially identical.
  • Formally, given adjacency matrix \(\mathrm{A}_1,\mathrm{A}_2\) and node features \(\mathrm{X}_1,\mathrm{X}_2\), then two graphs are isomorphic if and only if there exists a permutation matrix \(\mathrm{P}\) such that \(\mathrm{PA_1P^\top=A_2,PX_1=X_2}\)
• The challenges of graph isomorphism
  • The simple definition
  • Testing for graph isomorphism
    • A naive approach to test for isomorphism would involve the optimization problem 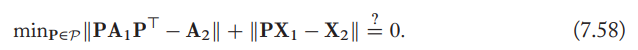with the computation complexity \(\mathcal{O}(|V|!)\).
    • Therefore, this is regarded as NP-indeterminate. No general polynomial time algorithms are known for this problem.
• Graph isomorphism and representational capacity
  • Graph isomorphism gives a way to quantify the representational power of different learning approaches. E.g., evaluating the power by asking how useful the representations would be for testing graph isomorphism.
  • In practice, no representation learning algorithm is going to be “perfect".

The Weisfieler-Lehman algorithm

• The steps of 1-WL

  

• The WL algorithm is known to converge in at most \(|V|\) iterations and is known to known to successfully test isomorphism for a broad class of graph.

• WL may fail for some graphs e.g. when the graph consists of multi disconnected subgraphs.

GNNs and the WL algorithm

• GNNs aggregate and update node embeddings using NNs while WL aggregates and updates discrete labels.

• Formally, the relation between GNNs and WL is

  

  It tells that GNNs are no more powerful than the WL algorithm when we have discrete information as node features.

• If the WL algorithm assigns the same label to two nodes, then any message-passing GNN will also assign the same embedding to these two nodes.

  

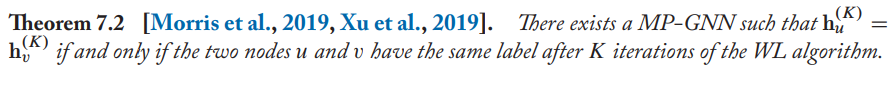
• If we define the message passing updates as

  

  then this GNN is sufficient to match the power of the WL algorithm.

• To make GNN is as powerful as WL, the aggregate and update function need to be injective, which means that they need to map every unique input to a unique output value. But this cannot be satisfied usually if the aggregate functions are using a average of the neighbor embeddings.

• GIN (graph isomorphism network) has few parameters but is still as powerful as the WL algorithm.

  • 

• In summary, MP-GNNs (message passing GNNs) are no more powerful than the WL algorithm.

Beyond the WL algorithm

• Relational pooling

  Considering the failure cases of the WL algorithm. Message passing approaches generally fail to identify closed triangles in a graph, which is a critical limitation.

  • To address the limitation, Murphy et al. consider MP-GNNs with unique node ID features. They simply add a unique, one-hot indicator feature (node ID) for each node.
    • However, this doesn't solve the problem and rather import a new and equally problematic issue that MP-GNNs is no longer permutation equivariant since the adding of node IDs. Specifically, assigning a unique ID to each node fixes a particular node ordering for the graph, which breaks the permutation equivariance.
  • The other way is Relational Pooling (PR) approach, which involves marginalizing over all possible node permutations. In practice, it will sum over all possible permutation matrices recovers the permutation invariance.
    • The limitation are
      • its computation complexity.
      • We have no way to characterize how much more powerful that PR-GNNs are.
    • But RP can achieve strong results using various approximation to decrease the computation cost.

• The \(k\)-WL test and \(k\)-GNNs

  Improving GNNs by adapting generalizations of the WL algorithm.

  • \(k\)-WL works on subgraphs in size \(k\), which can be used to test graph isomorphism by comparing the multi-sets for two graphs.
    • It introduces a hierarchy of representation capacity. For any \(k\ge2\) we have that the \((k+1)\)-WL test is strictly more powerful than the \(k\)-WL test.
    • To intimate this, Morris et al develop a \(k\)-GNN that is a differentiable and continuous analog of the \(k\)-WL algorithm. They learn embeddings associated with subgraphs, rather than noes, and the message passing occurs according to subgraph neighborhoods.
  • Graph kernel methods based on the \(k\)-WL test.

• Invariant and Equivariant \(k\) -order GNNs

  • MP-GNNs are equivariant to node permutations. And permuting the input to an MP-GNNs simply results in the matrix of output node embeddings being permuted in an analogous way.
  • MP-GNNs can also be permutation invariant at the graph level. The pooled graph-level embedding does not change when different node orderings are used.
  • Maron et al propose a general form of GNN-like models based on permutation equivariant/invariant tensor operations.
    • For a given input, both equivariant and invariant linear operators on this input will correspond to tensors that satisfy the fixed point in \(\mathrm{P}\star\mathcal{L}=\mathcal{L},\forall \mathrm{P}\in \mathcal{P}\), but the number of channels in the tensor will differ depending on whether it is an equivariant or invariant operator.
    • The fixed point can be constructed as a linear combination of a set of fixed basis elements.
    • The equivariant linear layers involve tensors that have up to \(k\) different channels.
    • Constructing \(k\)-order invariant models for \(k>3\) is generally computationally intractable. The built \(k\)-order GNNs are equally powerful as the \(k\)-WL algorithm.

Part III Generative Graph models

Chapter 8 Traditional graph generation approaches

The goal of graph generation is to build models that can generate realistic graph structures. The key challenge in graph generation is generating graphs that have certain desirable properties.

Traditional approaches to graph generation generally involve specifying some kind of generative process, which defines how the edges in a graph are created.

A more through survey and discussion is Newman's (1,12,13,108,109).

Erdos-Renyi model

• ER model may be the simplest and most well-known generative model of graphs. It simply assumes that the probability of an edge occurring between any pairs of nodes is equal to \(r\).
• To generate a random ER graph, just simply choose how many nodes we want, set the density parameter \(r\) and then use equation to generate the adjacency matrix.
• The downside of the ER model is that it doesn't generate very realistic graphs. The graph properties like degree distribution, existence of community structures, node clustering coefficients and tensors occurrence of structural motifs are not captured.

Stochastic block models

• SBMs seek to generate graphs with community structure.
• SBMs are based on blocks, every node has a probability that it belongs to block \(i\), edge probabilities are defined by a block-to-block probability matrix. To generate graph, for each node assign a class (block) by sampling and then sample edges for each pair of nodes.
• By controlling the edge probabilities within and between different blocks, one can generate graphs that exhibit community structure.
• The nodes have a probability \(\alpha\) of having an Eden with another node that assigned to the same community and a smaller probability of having an Eden with another node that is assigned to a different community.
• The variations including approaches for bipartite graphs, graphs with node features, as well as approaches to infer SBMs parameters from data.
• However, SBMs is limited in that it fails to capture the structural characteristic of individuals nodes that are present in most real-world graphs. In SBMs, the structure of individual communities is relatively homogeneous in that all the nodes have similar structural.

Preferential attachment

• Preferential attachment (PA) attempts to capture the inhomogeneous of communities (real-world degree distributions). It's built based on the assumption that many real-world graphs exhibit power-law degree distributions.

• The power law distributions are heavy tailed, which means that a probability distribution goes to zero for extreme values slower than an exponential distribution. It also means that there is a large number of nodes with small degrees but also have a small number of nodes with extremely large degrees.

• The steps of PA:

  

• The key idea is that the PA model connects new nodes to existing nodes with a probability that is proportional to the existing nodes' degrees.

• The generation process of PA is autoregressive, the edge probabilities are defined on an iterative approach.

Traditional applications

Historically, the methods introduced above have been used in two key applications:

• Generating synthetic data for benchmarking and analysis tasks
• Creating Null models
  • We can investigate the extent to which different graph characteristics are probable under different generative models.

The traditional approaches can generate graphs, but they lack the ability to learn a generative model from data.

Chapter 9 Deep generative models

Focus on the simple and general variants of VAEs, GANs and autoregressive models. All below will only focus on generating graph structure.

Variational autoencoder approaches

• Under VAEs, the key idea behind can be summarized as : the goal is to train a probabilistic decoder model from which one can sample realistic graphs by conditioning on a latent variable. Or to say, the goal is to learn a conditional distribution over adjacency matrices.

• The target is the decoder that generate graph from latent variable, but encoder and decoder are trained together.

• The components that required:

  • A probabilistic encoder model \(q_\phi\)

    It takes a graph as input. Generally , in VAEs the representation trick with Gaussian random variables is used to design this function.

  • A probabilistic decoder model \(p_\theta\)

    The decoder takes a latent representation as input and uses this input to specify a conditional distribution over graphs. Specifically, it defines a conditional distribution over the entries of the adjacency matrix.

  • A prior distribution over the latent space

    Usually a standard Gaussian prior is used.

• With these components, the loss is minimizing the evidence likelihood lower bound (ELBO)

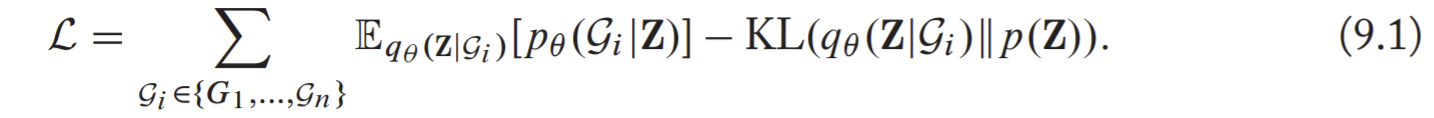  , with the basic idea that seek to maximize the reconstruction ability of the decoder.

  • The motivation behind the ELBO is rooted in the theory of variational inference.
  • The goals will be satisfied under this optimization method
    • The sampled latent representations encode enough information to allow our decoder to reconstruct the input.
    • The latent distribution is as close as possible to the prior. It's important if one wants to generate new graphs after training : they can generate new graphs by sampling from the prior and feeding these latent embeddings to the decoder.

Node-level latent

Encoding and decoding graphs based on node embeddings. The key idea is that the encoder generates latent representations for each node in the graph.

As a generative model, the node-level method is limited.

• Kipf et al. proposed VGAE (variational graph autoencoder)
  • Encoder model: can be based on any of the GNN architectures. In particular, two GNNs are used to generate mean (for each node in the input graph) and variance parameters separately. Once they are computed, tensors set of latent node embeddings can be sampled.
  • Decoder model: predict the likelihood of all the edges in the graph, given a matrix of sampled node embeddings. In VGAE, thy use a dot-product decoder.
  • The reconstruction error is a binary cross-entropy over the edge probabilities.
• Limitations: It's limited especially when a dot-product decoder is used. The decoder has no parameters, so the model is not able to generate non-trivial graph structures without a training graph as input.
• Grover et al. propose to augment the decoder with an iterative GNN based decoder.

Graph-level latent

The encoder and decoder functions are modified to work with graph-level latent representations.

• Encoder model: It can be an arbitrary GNN model augmented with a pooling layer. Again there are two separate GNNs to parameterize the mean and variance of a posterior normal distribution over latent variables.
• Decoder model: One original Graph-VAE model proposed to combine a basic MLP with a Bernoulli distributional assumption. Simply independent Bernoulli distribution for each edge, and the overall log-likelihood objective is equivalent to set of independent binary cross-entropy loss function on each edge.
  • The challenges while implementing with MLP:
    • Have to assume a fixed number of nodes
    • We don't know the correct ordering of the rows and columns in \(\tilde{A}\) when we are computing the reconstruction loss.
• Limitations: using graph-level latent representations introduces the issue of specifying node orderings. And with MLP, currently limits the application of the basic graph-level VAE to small graphs with hundred of nodes or less.

Adversarial approaches

VAE suffers from serious limitations--such as the tendency for VAEs to produce blurry outputs in the image domain.

• Some works
  • De Cao and Kipf et al. propose one that is similar to the graph-level VAE.
    • The generator is a MLP that generates a matrix of edge probabilities given a seed vector.
    • The discrete adjacency matrix is generated by sampling independent Bernoulli variables for each edge.
    • The discriminator employ any GNN-based graph classification model.
• Benefits: GAN-based methods remove the complication of specifying a node ordering in the loss computation as long as the discriminator model is permutation invariant.
• Limitations : GAN-based approaches to graph generation have so far received less attention and success than their variational counterparts.

Autoregressive methods

Both VAE-based approaches and basic GANs that discussed before use simple MLPs to generate adjacency matrices. Autoregressive methods can decode graph structures from latent representations, they will combine GANs and VAEs.

Modeling edge dependencies

Previous it's assumed that the edges are independent for convenience, but this is not true in real world.

• In autoregressive model, it's assumed that edges are generated sequentially and that the likelihood of each edge can be conditioned on the edges that have been previously generated.

• Assume the lower-triangular portion of the adjacency matrix \(\mathrm{A}\) is denoted as \(\mathrm{L}\).

  

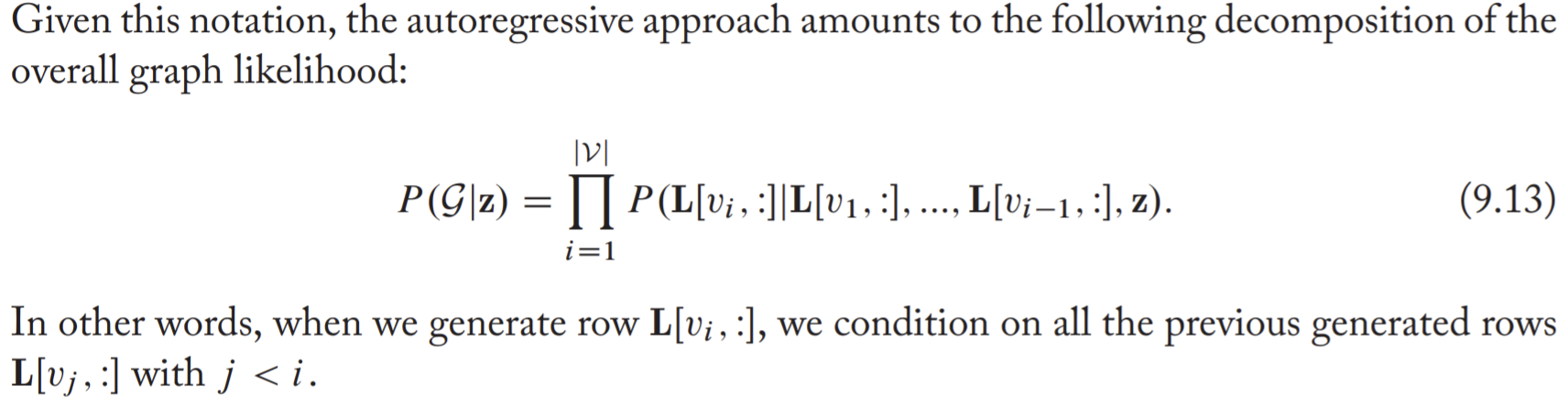
Recurrent models for graph generation

• GraphRNN : use a hierarchical RNN to model the edge dependencies.
  • The 1st RNN in this model is a graph-level RNN that is used to model the state of the graph that has been generated so far. It involves a stochastic sampling process to generate the discrete edges. In this way, the graph RNN is able to generate diverse samples of graphs even when a fixed initial embedding is used.
  • The 2nd RNN, termed a the node-level RNN, generates the entries of \(\mathrm{L}\) lower triangular adjacency matrix in an autoregressive manner. It will take the graph-level hidden state as its input and then sequentially generate the binary values of \(\mathrm{L}\), assuming a conditional Bernoulli distribution for each entry.
  • The node level RNN is initialized at each time-step with the current hidden state of the graph-level RNN.
  • Both RNNs can be optimized to maximize the likelihood of the training graphs using the teaching forcing strategy, meaning that the ground truth of \(\mathrm{L}\) are always used to update the RNNs during training. But computing the likelihood requires the assumption that a particular a ordering over the generated nodes.
  • It's more capable of generating grid-like structures, compared to the basic graph-level VAE.
  • Limitations: It still generates unrealistic artifacts (e.g. long chains) when trained on samples of grids. It can be difficult to train and scale to large graphs due to the need to backpropagate through many steps of RNN recurrence.
• GRAN: generate graphs by using a GNN to condition on the adjacency matrix that has been generated so far. GRAN models dependencies between edges. It maintains the autoregressive decomposition of the generation process.
  • It uses GNNs to model the autoregressive generation process.
  • One can model the conditional distribution of each row of the adjacency matrix by running a GNN on the graph that has been generated so far.
  • Since there are no node attributes associated with the generated nodes, the input feature matrix \(\tilde{\mathrm{X}}\) to the GNN can simply contain randomly sampled vectors.
  • The key benefit of GRAN compared with GraphRNN is that it does not need to maintain a long and complex history in a graph-level RNN.
  • To use GRAN on large graphs, one improvement is that multiple nodes can be added simultaneously in a single block rather than adding nodes one at a time.

Evaluating graph generation

Quantitatively compare the different models introduced previouly?

• Currently is to analyze different statistics of the generated graphs and to compare the distribution of statistics for the generated graphs to a test set.
• Compute the distance between the statistic's distribution on the test graph and generated graph using a distributional measure, such as the total variation distance.
• The statistics that are used including degree distributions, graphlets counts, and spectral features with distributional distances computed using variants of the total variation score and the 1st Wassertein distance.

Molecule generation

• The goal of molecule generation is to generate molecular graph structures that are both valid (e.g., chemically stable) and ideally have some desirable properties (e.g., medicinal properties or solubility).
• Domain-specific knowledge for both model design and evaluation.

Conclusion

• Building models that can infer latent graph structures beyond the input graph that we are given is a critical direction for pushing forward graph representation learning.
• Message-passing GNNs are inherently bounded by the WL isomorphism test. They suffer from over-smoothing, being limited to simple convolutional filters, and being restricted to tree-structured computation graphs.