Paper--Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition

Paper Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition

Code here

Why?

Previous work

• Human action recognition: can be solved by appearance, depth, optical flows, and body skeletons.
• Models for graph
  • Recurrent neural networks
  • GNNs:
    • Spectral perspective: the locality of the graph convolution is considered in the form of spectral analysis.
    • Spatial perspective: the convolution filters are applied directly on the graph nodes and their neighbors.
• Skeleton Based Action Recognition
  • Handcrafted feature based methods: design several handcrafted features to capture the dynamics of joint motion. E.g., covariance matrices of joint trajectories, relative positions of joints, rotations and translations between body parts.
  • Deep learning methods: recurrent neural networks and temporal CNNs. Many emphasize the importance of modeling the joints within parts of human bodies.

Summary

• Observations
  • Earlier methods of using skeletons for action recognition simply employ the joint coordinates at individual time steps to form feature vectors, and apply temporal analysis thereon. They do not explicitly exploit the spatial relationships among the joint.
  • Most existing methods which explore spatial relationship rely on hand-crafted parts or rules to analyze the spatial patterns.
  • Traditional CNNs are not suitable for 2D or 3D skeletons (graphs rather than data in grids).
• Limitations:
  • Conventional approaches for modeling skeletons usually rely on hand-crafted parts or traversal rules, thus resulting in limited expressive power and difficulties of generalization.
  • Models using hand-crafted parts are difficult to be generalized to others
  • These parts used in DL based methods are usually explicitly assigned using domain knowledge, which is not automatic and practical.

Goals

Build a better model for dynamics of human body skeletons. Specifically, a new method that can automatically capture the patterns embedded in the spatial configuration of the joints as well as the temporal dynamics is required.

How?

Idea

Skeletons in frames are connected as natural spatial-temporal graph, then using GCN.

Data Preparation

• The feature vector on a node \(F(v_{ti})\) consists of coordinate vectors, as well as estimation confidence, of the i-th joint on frame t.
• Construct the spatial temporal graph on the skeleton sequences in two steps. First, the joints within one frame are connected with edges according to the connectivity of human body structure. Then each joint will be connected to the same joint in the consecutive frame.
• Both 18 joints skeleton model or 25 joints skeleton model work fine.

Implementation

• Model

  

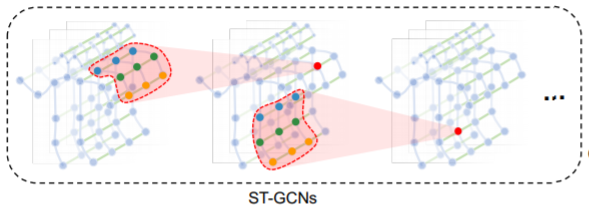
  ResNet mechanism is applied on each ST-GCN unit.

  Layer name	configuration
  \(1\sim3\)	64 channels
  \(4\sim6\)	128 channels
  \(7\sim9\)	256 channels, 9 temporal kernel size
  Global pooling+softmax

• Loss function

  • Sampling function \(\mathbb{p}\) enumerates the neighbors of location \(x\).

    

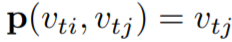
    In this paper, the 1-neighbor set of joint nodes are used.

  • The filter weights \(\mathrm{w} (v_{ti},v_{tj})\) are shared everywhere on the input image.

    Build a mapping \(l_{ti}:B(v_{ti})\rightarrow\{0,\cdots,K−1\}\) which maps a node in the neighborhood to its subset label. The weight function \(\mathrm{w}(v_{ti}, v_{tj}):B(v_{ti})\rightarrow R^c\) can be implemented by indexing a tensor of \((c,K)\) dimension or

    \(\mathrm{w}(v_{ti},v_{tj})=\mathrm{w}'(l_{ti}(v_{tj})\)

    • Labeling strategies (the definition of \(l_{ti}\))

      

      • Uni-labeling

        Make the whole neighbor set itself as subset. Then feature vectors on every neighboring node will have a inner product with the same weight vector. Formally, \(K=1,l_{ti}(v_{tj})=0,\forall i,j\in V\)

      • Distance partitioning

        \(d=0\) refers to the root node itself and remaining neighbor nodes are in the \(d =1\) subset. Formally , \(K=2,l_{ti}(v_{tj})=d(v_{tj},v_{ti})\)

      • Spatial configuration partitioning

        Three subsets: 1) the root node itself; 2)centripetal group and 3) centrifugal group.

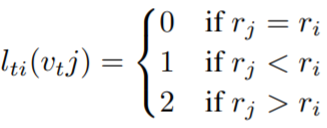        , where \(r_i\) is the average distance from gravity center to joint \(i\) over all frames in the training set.

    • Learnable edge importance weighting

      One joint appears in multiple body parts should have different importance in modeling the dynamics of these parts. A learnable mask M is added on every layer of spatial temporal graph convolution.

  • The spatial graph convolution

    \(f_{out}(v_{ti})=\sum\limits_{v_{tj}\in B(v_{ti})}\frac{1}{Z_{ti}(v_{tj})}f_{in}(\mathbb{p}(v_{ti},v_{tj}))\cdot \mathrm{w}(v_{ti},v_{tj})=\\\sum\limits_{v_{tj}\in B(v_{ti})}\frac{1}{Z_{ti}(v_{tj})}f_{in}(v_{tj})\cdot \mathrm{w}(l_{ti}(v_{tj}))\), \(Z_{ti}(v_{tj})=|\{v_{tk}|l_{ti}(v_{tk})=l_{ti}(v_{tj})\}|\) is the cardinality of the corresponding subset. It's for balancing the contributions of different subsets to the output.

  • Spatial temporal modeling

    Extend neighbors so as to include temporally connected joints

    \(B(v_{ti})={v_{qj}|d(v_{tj},v_{ti})\le K,|q-t|\le \lfloor\Gamma/2\rfloor}\), where \(\Gamma\) is temporal kernel size (controls the temporal range to be included in the neighbor graph). Then , the sampling function is \(l_{ST}(v_{qj})=l_{ti}(v_{tj})+(q-t+\lfloor\Sigma/2\rfloor)\times K\).

  • The final convolution formula:

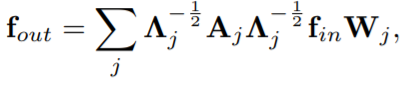    , where \(\Lambda_j^{ii}=\sum_k(A_j^{ik})+\alpha\), \(\alpha=0.001\) is to avoid empty rows in \(A_j\). To add learnable mask \(M\), displace \(A_j\) as \(A_j\otimes M\).

• Why does it work?

  • Parts restrict the modeling of joints trajectories within “local regions” compared with the whole skeleton, thus forming a hierarchical representation of the skeleton sequences.

Experiments

• Dataset:

  • Kinetics (unconstrained action recognition dataset), provides only raw video clips without skeleton data.

    • Augmentation: To avoid overfitting,two kinds of augmentation are used to replace dropout layers when training on the Kinetics dataset. 1) affine transformations, 2) sampling part of the frames from the whole frame and testing by a whole frame. May that's a way for avoiding the two consecutive frame are too similar?

    • Videos to skeletons

      To work on skeletons, openpose is used for extracting. Concretely, resize all videos to the resolution of 340 × 256 and convert the frame rate to 30 FPS. Then OpenPose toolbox is used to estimate the location of 18 joints on every frame of the clips.

    • Final features:

      Finally the clips are represented by a tensor in shape \((3,T,18,2)\), where 18 is the number of joints, 2 is the number of people and 3 is the number of features (X,Y,C), C is the confidence.

  • NTU-RGBD ( in-house captured action recognition dataset)

    • Already annotated with 25 3D joints
    • Each clip is guaranteed to have at most 2 subjects

• Training: SGD with a learning rate of 0.01. \(lr\) decay by 0.1 after every 10 epochs.

• Evaluation metrics

  • Kinetics

    Test on validation set. Using top-1 and top-5 classification accuracy

  • NTU-RGBD

    Report top-1 recognition accuracy.

    • Cross-subject: Train on one subset of actors and test on the remaining actors.
    • Cross-view: Train on skeletons from camera views 2 and 3, and test on those from camera view 1.

Ablation study

Applied on Kinetics dataset.

• Spatial temporal graph convolution

  Model	configuration
  baseline-TCN	squeeze Spatial dimension, concatenate all input joint locations to form the input features at each frame \(t\).
  local convolution	The input data are the same format, but with unshared convolution filters.

• Partition strategies: same as what described before. Distance partitioning* is as intermediate between the distance partitioning and uni-labeling. The filters in this setting only differs with a scaling factor -1, or to say \(\mathrm{w}_0=-\mathrm{w}_1\).

• Learnable edge importance weighting

  This setting is named as ST-GCN+Imp.

• Results

  

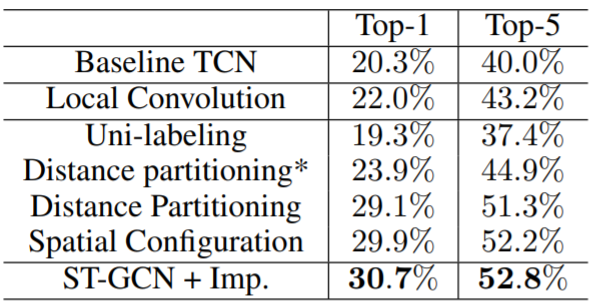
  • Better performance of ST-GCN based models could justify the power of the spatial temporal graph convolution in skeleton based action recognition
  • Distance partitioning* achieves better performance than uni-labeling, which again demonstrate the importance of the partitioning with multiple subsets.
  • ST-GCN model with learnable edge importance weights can learn to express the joint importance.

Compared with SOTA

Model setting: ST-GCN+Learnable weights+Spatial configuration partitioning

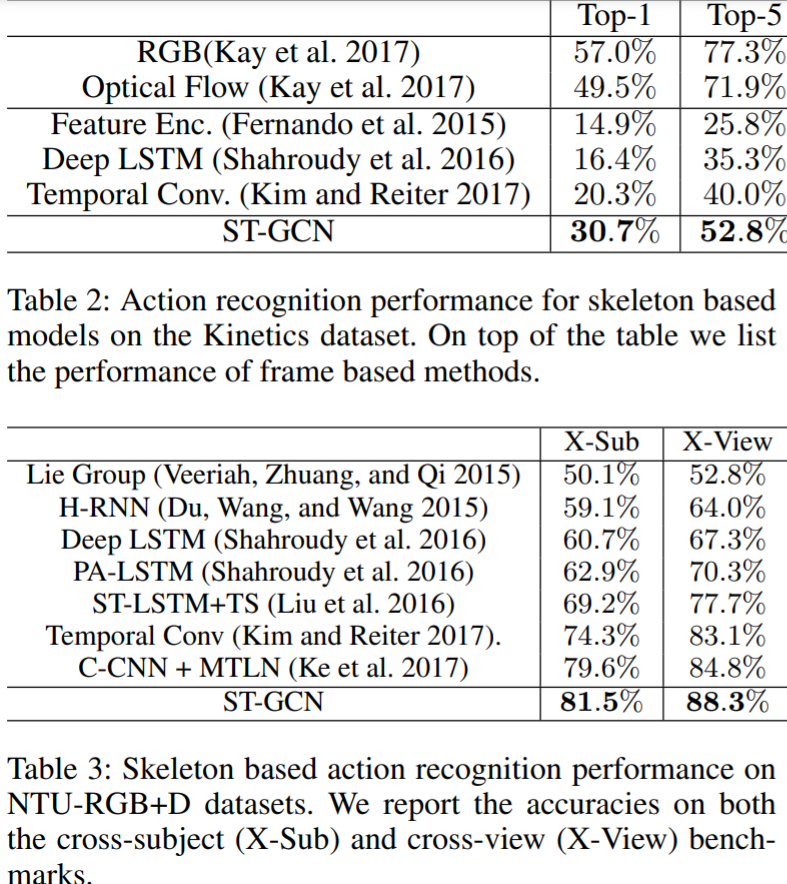
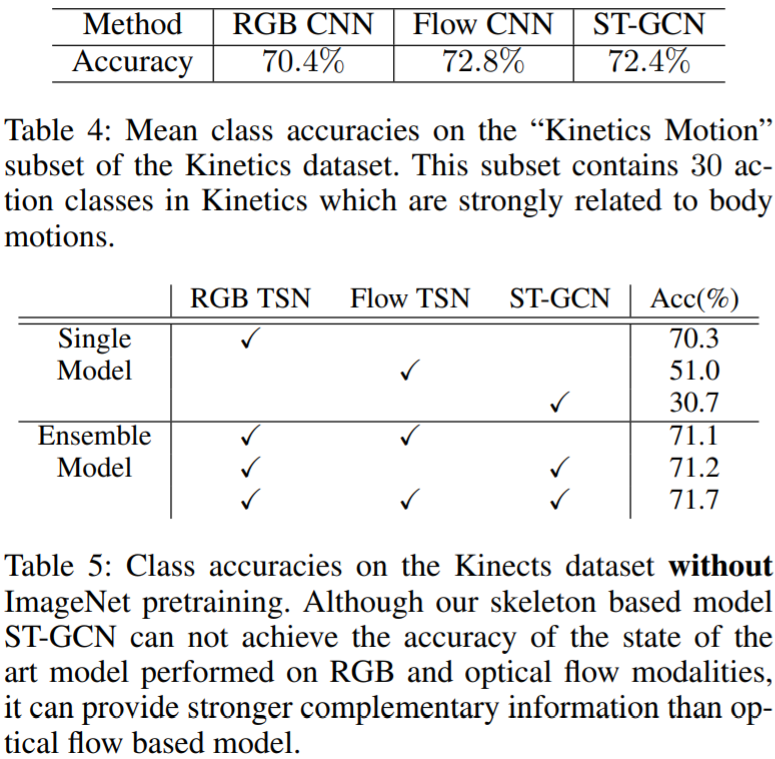
• Kinetics: ST-GCN is able to outperform previous representative approaches, but under-perform methods in RGB or optical flow.
• NTU-RGBD: No data augmentation before training. It outperforms all other selected candidates.
• The skeleton based model ST-GCN can provide complementary information to RGB and optical flow models.

Conclusion

• Propose ST-GCN, a generic graph-based formulation for modeling dynamic skeletons, which is the first that applies graph-based neural networks for action recognition.
• Propose several principles in designing convolution kernels in ST-GCN to meet the specific demands in skeleton modeling.
• On two large scale datasets for skeleton-based action recognition, the proposed model achieves superior performance as compared to previous methods using hand-crafted parts or traversal rules, with considerably less effort in manual design.