Paper--Self-supervised Learning on Graphs, Deep Insights and New Directions

2021-01-11

Paper Self-supervised Learning on Graphs: Deep Insights and New Directions

Codes

Why?

Nodes in graphs present unique structure information and they are inherently linked indicating not independent and identically distributed (or i.i.d.).
(SSL) has been introduced in both the image and text domains to alleviate the need of large labeled data by deriving labels for the significantly more unlabeled data.
To fully exploit the unlabeled nodes for GNNs, SSL can be naturally harnessed for providing additional supervision.
The challenges of graph to use SSL:
- graphs are not restricted to these rigid structures.
- each node in a graph is an individual instance and has its own associated attributes and topological structures
- instances (or nodes) are inherently linked and dependent of each other.

Goals

Focus on advancing GNNs for node classification where GNNs leverage both labeled and unlabeled nodes on a graph to jointly learn node representations and a classifier that can predict the labels of unlabeled nodes on the graph. Aims at gain insights on when and why SSL works for GNNs and which strategy can better integrate SSL for GNNs.
Focus on semi-supervised node classification task

\(\min\limits_{\theta}\mathcal{L}_{task}(\theta,\mathrm{A,X},\mathcal{D}_L)=\sum\limits_{(v_i,y_i)\in\mathcal{D}_L}\ell(f_{\theta}(\mathcal{G})_{v_i},y_i)\)

Previous work

Examples

Multi-stage self-supervised learning for graph convolutional networks on graphs with few labels utilize the clustering assignments of node embeddings as guidance to update the graph neural networks.
Self-supervised graph representation learning via global context prediction proposed to use the global context of nodes as the supervisory signals to learn node embeddings.

Basic pretext task on graphs

Structure information (Adjacency matrix \(\mathrm{A}\))

Construct self-supervision information for the unlabeled nodes based on their local structure information, or how they relate to the rest of the graph

Local structure information

Node property
- use node degree as a representative local node property for self-supervision while leaving other node properties (or the combination) as one future work
- Formally, let \(d_i=\sum\limits_{j=1}^{N}\mathrm{A}_{ij}\) denote the degree of \(v_i\) and construct the associated loss of the SSL pretext task as
  
  \(\mathcal{L}_{self}(\theta',\mathrm{A,X},\mathcal{D}_U)=\frac{1}{|\mathcal{D}_U|}\sum\limits_{v_i\in\mathcal{D}_U}(f_{\theta'}(\mathcal{G})_{v_i}-d_i)^2\), where \(\mathcal{D}_U\) denote the set of unlabeled nodes and associated pretext task labels in the graph.
- Assumption: The node property information is related to the specific task of interest.
EdgeMask
- Build pretext task based on the connections between two nodes in the graph. Specifically, one can first randomly mask some edges and then the model is asked to reconstruct the masked edges.
- Formally, first mask \(m_e\) edges denotes as the set \(\mathcal{M}_e\subset\varepsilon\) and also sample the set \(\bar{\mathcal{M}_e}=\{(v_i,v_j)|v_i,v_j\in\mathcal{V},(v_i,v_j)\notin\varepsilon\}\), \(|\bar{\mathcal{M}_e}|=|\mathcal{M}_e|=m_e\) . Then the SSL pretext task is to predict whether there exist a link between a given node pair.
  
  \(\mathcal{L}_{self}(\theta',\mathrm{A,X},\mathcal{D}_U)=\\\frac{1}{|\mathcal{M}_e|}\sum\limits_{(v_i,v_j)\in\mathcal{M}_e}\ell(f_w(|f_{\theta'}(\mathcal{G})_{v_i}-f_{\theta'}(\mathcal{G})_{v_j}|),1)+\frac{1}{|\bar{\mathcal{M}_e}|}\sum\limits_{(v_i,v_j)\in\bar{\mathcal{M}_e}}\ell(f_w(|f_{\theta'}(\mathcal{G})_{v_i}-f_{\theta'}(\mathcal{G})_{v_j}|),0)\), where \(\ell(\cdot,\cdot)\) is the cross entropy loss, \(f_w\) linearly maps to 1-dimension.
- Expecting to help GNN learn information about local connectivity.

Global structure information

Not only based on the node itself or limited to its immediate local neighborhood, but also considering the position of the node in the graph.

PairwiseDistance
- Maintain global topology information through a pairwise comparison. Or to say, pretext task will be able to distinguish/predict the distance between different node pairs.
- The measurements of distance vary.
- If use the shortest path length \(p_{ij}\) as a measure of the distance, then for all node pairs \(\{(v_i,v_j)|v_i,v_j\in\mathcal{V}\}\), they are grouped into four categories: \(p_{ij}=\{1,2,3,\ge4\}\), \(4\) is because of the computing price and accuracy (the more neighbors , the more unrelated noises are included.) Practically, randomly sample a certain amount of node pairs \(S\) used for SSL during epoch. Then the SSL loss is \(\mathcal{L}_{self}(\theta',\mathrm{A,X},\mathcal{D}_U)=\frac{1}{|S|}\sum\limits_{(v_i,v_j)\in S}\ell(f_w(|f_{\theta'}(\mathcal{G})_{v_i}-f_{\theta'}(\mathcal{G})_{v_j}|),C_{p_{ij}})\), where \(C_{p_{ij}}\) is the corresponding distance category of \(p_{ij}\).
Distance2Clusters
- Predicting the distance from the unlabeled nodes to predefined graph clusters. Thus enforce the representations to learn a global positioning vector of each of the nodes.
- First partitioning the graph to get \(k\) clusters \(\{C_1,C_2,\cdots,C_k\}\) by METIS graph partitioning methods. Denote the node with highest degree as center node \(c_j\) in each cluster.
- Formally, the SSL will optimize \(\mathcal{L}_{self}(\theta',\mathrm{A,X},\mathcal{D}_U)=\frac{1}{|\mathcal{D}_U|}\sum\limits_{v_i\in\mathcal{D}_U}\|f_{\theta'}(\mathcal{G})_{v_i}-d_i\|^2\), where \(\mathrm{d}_i\) is the distance vector between node \(v_i\) and each center.

Attribute information (Nodes matrix \(\mathrm{X}\))

Guide the GNN to ensure certain aspects of node/neighborhood attribute information is encoded in the node embeddings after a SSL attribute-based pretext.

AttributeMask
- Let GNN learn attribute information via pretext
- Randomly mask (e.g. set to zero ) the features of \(m_a\) nodes \(\mathcal{M}_a\subset\mathcal{V}, |\mathcal{M}_a|=m_a\), then SSL will try to construct these features. Formally , \(\mathcal{L}_{self}(\theta',\mathrm{A,X},\mathcal{D}_U)=\frac{1}{|\mathcal{M}_a|}\sum\limits_{v_i\in\mathcal{M}_a}\|f_{\theta'}(\mathcal{G})_{v_i}-\mathrm{x}_i\|^2\), where \(\mathrm{x}_i\) is the dense features after PCA.
PairewiseAttrSim
- The similarity two nodes have in the input feature space is not guaranteed in the learned representations due to the GNN aggregating features from the two nodes local neighborhoods.
- Specifically,
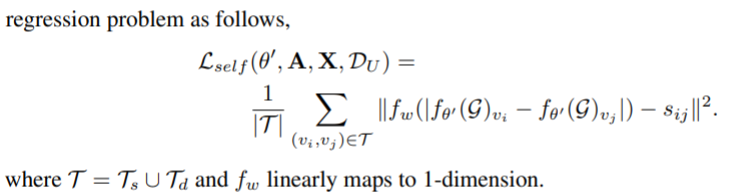
- Only constrain the intra-class distance

Merge pretext task on Graphs

Joint Training
- Optimize the SSL loss (i.e., \(\mathcal{L}_{self}\)) and supervised loss (i.e., \(\mathcal{L}_{task}\)) simultaneously.
- The overall objective is \(\min\limits_{\theta,\theta'}\mathcal{L}_{task}(\theta,\mathrm{A,X},\mathcal{D}_L)+\lambda(\theta',\mathrm{A,X},\mathcal{D}_U)\), where \(\lambda\) is the hyperparameter to control the distribution of self-supervision.
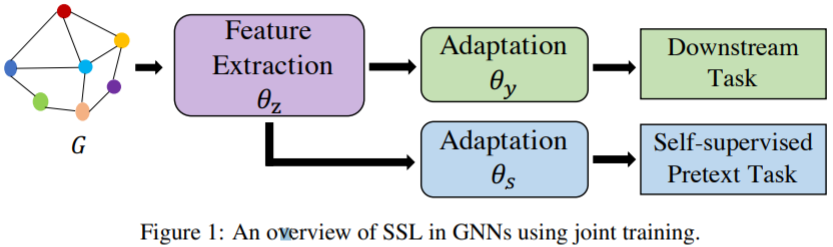
Two-stage training

Fine tuning the model which is pretrained on pretext task on downstream dataset.

Analysis

Targets: Understand what SSL information works for GNNs, which strategies can better integrate SSL for GNNs, and further analyze why SSL is able to improve GNNs
Datasets: Cora, Citeseer, Pubmed
Training: Adam, learning rate \(0.01\), \(L_2\) regularization \(5e-4\), dropout rate \(0.5\), \(128\) hidden units across all self-supervised information and GCN, top-K=bottom-K=\(3\). \(\lambda\) in range \(\{0,0.001,0.01,0.1,1,5,10,50,100,500,1000\}\), \(m_e,m_a\) in \(\{10\%,20\%\}\) the size of \(|V|\).
Two-stage training
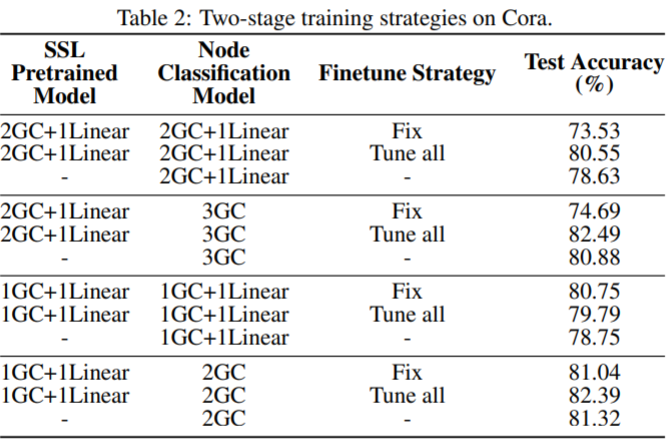
- the configuration of one graph convolutional layer for feature extraction, one graph convolutional layer for the adaptation of node classification and one linear layer for the adaptation of pretext task works very well for all three strategies
- In most cases, the strategy of “Tune all" achieves the best performance--> fine tune for downstream task is necessary.
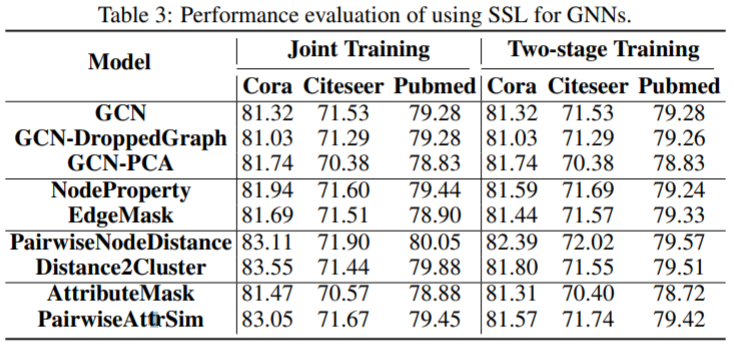
SSL for GNNs
- Joint training vs. Two-stage Training
  
  Joint training outperforms the Two-stage training in most settings.
- What SSL works for GNNs
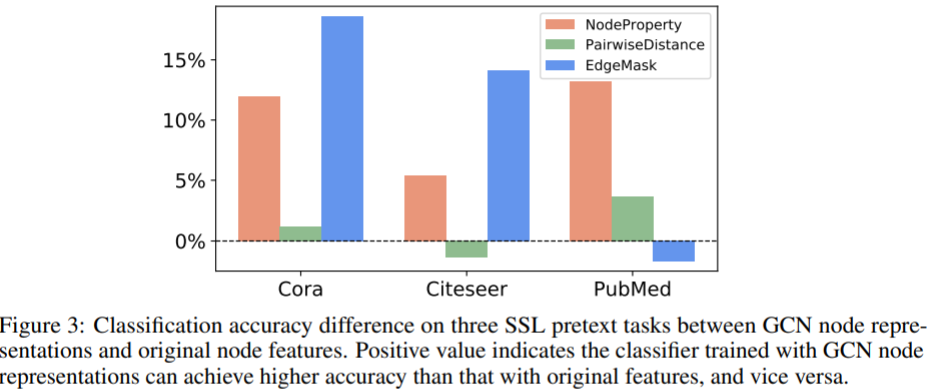
  - SSL for GNNs will improve the accuracy for downstream task
  - Across all datasets , the best performing method is a pretext task developed from global structure information.
  - self-supervised information from both the structure and attributes have potentials
  - For the structure information, the global pretext tasks are likely to provide much more significant improvements compared to the local ones.
- Why SSL Works for GNNs
  - GCN for node classification is naturally semi-supervised that has explored the unlabeled nodes, those (SSL pretext) failed to improve GCNs is argued resulted in GCN has already learned that information.
  - GCN is unable to naturally learn the global structure information and employing pairwise node distance prediction as the SSL task can help boost its performance for the downstream task.
- The capability of pretext representations maintaining similarity
  
  The most popular similarity for graph is structural equivalence and regular equivalence (规则的等效节点是那些不一定具有相同邻居但具有自身相似的邻居的节点).
  - Authors argue pretext task can maintain these two similarities by changing the definition of task (like nodes attribute task or distance between a pair of nodes can maintain structure similarity and regular equivalence.

Advanced pretext task on graphs

Pretext tasks are built with the intuition of adapting the notion of regular equivalence to having neighbors with similar node labels (or regular task equivalence). Specifically, if every node constructs a pretext vector based on information in regards to the labels from their neighborhood, then two nodes having similar (or dissimilar) vectors will be encouraged to be similar (or dissimilar) in the embedding space.

Proposed Tasks

Distance2Labeled

Modify Distance2Cluster. Propose to predict the distance vector from each node to the labeled nodes (i.e., \(\mathcal{V}_L\)) as the pretext task. For class \(c_j\in\{1，\cdots,K\}\) and unlabeled node \(v_i\in\mathcal{V}_U\), the distance vector \(\mathrm{d}_i\) for node \(v_i\) is defined as three shortest path length (average, minimum, maximum) from \(v_i\) to all labeled nodes in class \(c_i\).
Formally, the objective is \(\mathcal{L}_{self}(\theta',\mathrm{A,X},\mathcal{D}_U)=\frac{1}{|\mathcal{D}_U|}\sum\limits_{v_i\in\mathcal{D}_U}\|f_{\theta'}(\mathcal{G})_{v_i}-d_i\|^2\).

ContextLabel

Considering the sparsity of labels, use similarity based function which utilize structure , attributes , and the current labeled nodes to construct a neighbor label distribution context vector \(\bar{\mathrm{y}}_i\) for each nodes as follows: \(f_s({\mathrm{A,X},\mathcal{D}_L,\mathcal{V}_U})\rightarrow\{\bar{\mathrm{y}}_i|v_i\in\mathcal{V}_U\}\). Specifically , the \(c\)-th item of \(\bar{\mathrm{y}}\) is: \(\bar{\mathrm{y}}_{ic}=\frac{|\mathcal{N}_{\mathcal{V}_L}(v_i,c)|+|\mathcal{N}_{\mathcal{V}_U}(v_i,c)|}{|\mathcal{N}_{\mathcal{V}_L}(v_i)|+|\mathcal{N}_{\mathcal{V}_U}(v_i)|},c=1,\cdots,K\). (For the neighbors of node \(v_i\) (including unlabeled and labeled neighbors), the ratio of neighbors in class \(c\))
Formally, the objective is \(\mathcal{L}_{self}(\theta',\mathrm{A,X},\mathcal{D}_U)=\frac{1}{|\mathcal{D}_U|}\sum\limits_{v_i\in\mathcal{D}_U}\|f_{\theta'}(\mathcal{G})_{v_i}-\mathrm{y}_i\|^2\)
The labels of nodes (aka \(f_s\)) can be generated by LP (Label propagation ) or ICA (Iterative Classification Algorithm). But these will import weak labels that are too noisy.

EnsembleLabel

Ensemble various functions \(f_s\). \(\bar{y}_i=\arg\max_c\sigma_{LP}(v_i)+\sigma_{ICA}(v_i),c=1,\cdots,K\)
The objective is the same as ContextLabel method.

CorrectedLabel

Enhance ContextLabel by iteratively improving the context vectors. GNN \(f_{\theta}\) is trained on both the original (e.g., \(\bar{\mathrm{y}}_i\)) and corrected (e.g., \(\hat{\mathrm{y}}_i\)) context distributions.
Formally, the loss is \(\mathcal{L}_{self}(\theta',\mathrm{A,X},\mathcal{D}_U,\hat{\mathcal{D}}_U)=\\\frac{1}{|\mathcal{D}_U|}\sum\limits_{v_i\in\mathcal{D}_U}\|f_{\theta'}(\mathcal{G})_{v_i}-\bar{\mathrm{y}}_i\|^2+\alpha(\frac{1}{|\mathcal{D}_U|}\sum\limits_{v_i\in\mathcal{D}_U}\|f_{\theta'}(\mathcal{G})_{v_i}-\hat{\mathrm{y}}_i\|^2)\), where the 1st and second terms are to fit the original and corrected context distributions respectively, and \(\alpha\) controls the contribution from the corrected context distribution. \(\hat{y}_i=\arg\max_c\frac{1}{p}\sum\limits_{l=1}^p\cos(f_{\theta'}(\mathcal{G})_{v_i},\mathrm{z}_{cl}),c=1,\cdots,K\). Where \(p\) indicates the prototype nodes in top-\(p\) largest \(\rho\) values, indicating the nodes if the measurements (\(\rho\)) of their neighbors' label similarity is in top-\(p\).. Concretely, the similarity of labels' similarity is defined as \(\rho_i=\sum\limits_{j=1}^m\mathrm{sign}(\mathrm{S}_{ij}-S_c)\), where \(\mathrm{S}_{ij}\) is the cosine similarity between two nodes based on their embeddings, \(S_c\) indicating a constant value (which is selected as the value rank in top \(40\%\) in \(\mathrm{S}\)).
In other words, the average similarity between \(v_i\) and \(p\) prototypes is used to represent the similarity between \(v_i\) and the corresponding class, and then assign the class \(c\) having the largest similarity to \(v_i\).

Experiments for evaluating

Experiment settings
- Datasets: Cora, Citeseer, Pubmed and Reddit
- Model: 2-layer GCN as the backbone, with hidden units of 128, \(L_2\) regularization \(5e−4\), dropout rate \(0.5\) and learning rate \(0.01\). For the SSL loss, the hidden representations from the first layer of GCN are fed through a linear layer to solve SSL pretext task. Jointly train SSL and GCNs. \(\lambda\) ranges in \(\{1, 5, 10, 50, 100, 500\}\). \(\alpha\) ranges in \(\{0.5, 0.8, 1, 1.2, 1.5\}\).
- Measurements: the average accuracy with standard deviation.
Analysis
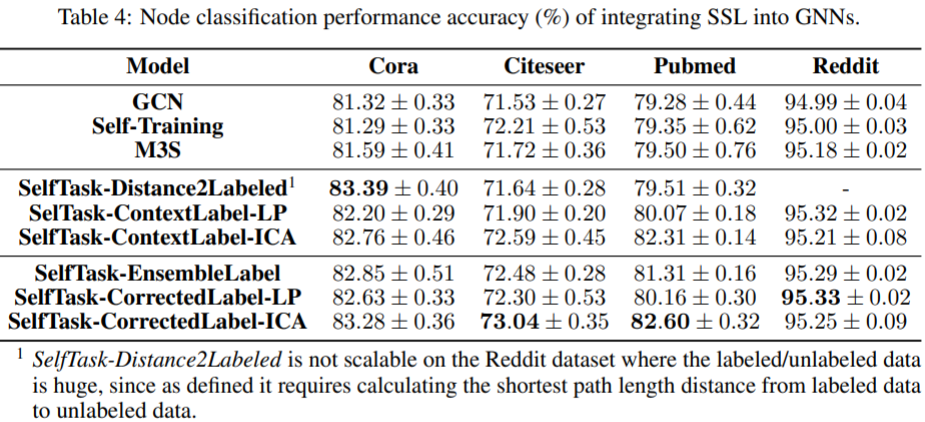
- Performance comparison: Though they argue the performance exist, but seems not that significant. They summarize: label correction can better extend label information to unlabeled nodes than ensemble, but it's much less inefficient. A tradeoff must be taken in.
- Fewer Labeled Samples
  - By randomly sampling 5 or 10 nodes per class for training and the same number of nodes for validation.
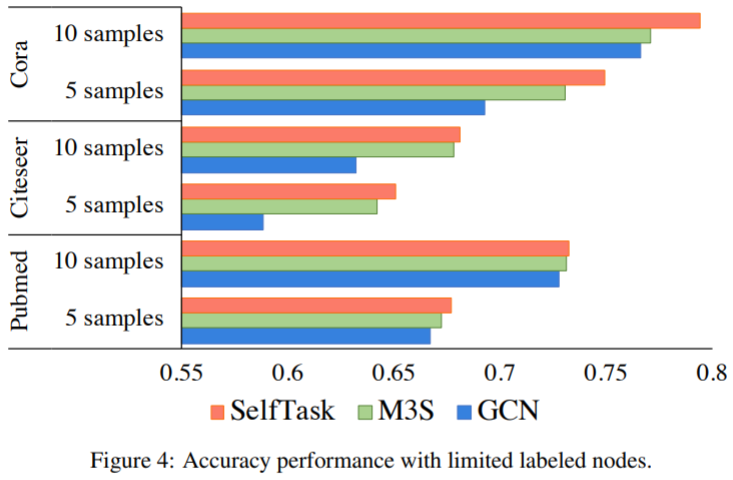
  - SelfTask achieves even greater improvement when the labeled samples are fewer and consistently outperforms the state-of-the-art baselines.
  - Why with fewer samples per class SelfTask can be even better?
- Parameter Analysis
  - Only the sensitivity of the best model SelfTaskCorrectedLabel-ICA is evaluated. Vary \(\lambda\) in the range of \(\{0, 0.1, 0.5, 1, 5, 10, 50, 100\}\) and \(\alpha\) from 0 to 2.5 with an interval of 0.25.
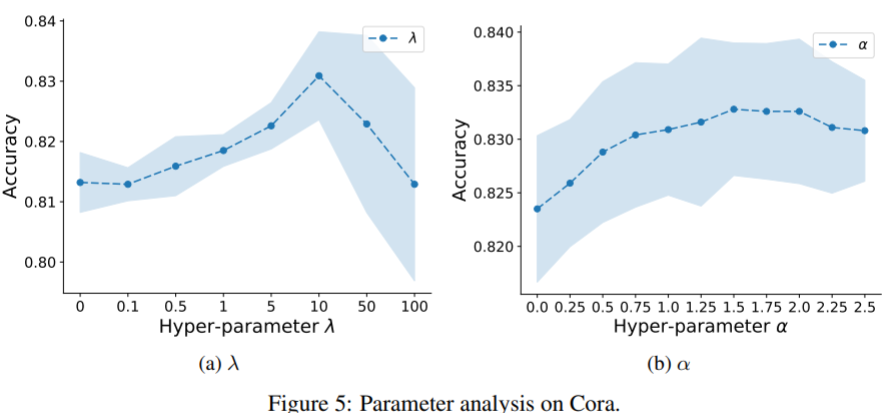
  - The performance of this model first increases with the increase of \(\lambda\), which controls the contribution of SSL pretext task.
  - The using of correction is confirmed.
  - They don't report sensitivity on other datasets, which should have been in supplementary.

Conclusion

Present detailed empirical study to understand when and why SSL works for GNNs and which strategy can better work with GNNs.
Propose a new direction SelfTask to build advanced pretext tasks which further exploit task-specific self-supervised information, and demonstrate that our advanced method achieves state-of-the-art performance.