Paper Predicting What You Already Know Helps: Provable Self-Supervised Learning
Why?
Previous work
Pretext tasks
- Reconstruct images from corrupted versions or just part it: including denoising auto-encoders, image inpainting, and split-brain autoencoder
- Using visual common sense, including predicting rotation angle, relative patch position, recovering color channels, solving jigsaw puzzle games, and discriminating images created from distortion.
- Contrastive learning: learn representations that bring similar data points closer while pushing randomly selected points further away or maximize a contrastive-based mutual information lower bound between different views
- Create auxiliary tasks: The natural ordering or topology of data is also exploited in video-based, graph-based or map-based self-supervised learning. For instance, the pretext task is to determine the correct temporal order for video frames.
Theory for self-supervised learning: contrastive learning
- Contrastive learning may not work when conditional independence holds only with additional latent variables
Theory Limitations Shows shows guarantees for contrastive learning representations on linear classification tasks using a class conditional independence assumption Not handle approximate conditional independence Contrastive learning representations can linearly recover any continuous functions of the underlying topic posterior under a topic modeling assumption for text The assumption of independent sampling of words that they exploit is strong and not generalizable to other domains like images Studies contrastive learning on the hypersphere through intuitive properties like alignment and uniformity of representations No connection made to downstream tasks A mutual information maximization view of contrastive learning Some issues point by paper [45] Explain negative sampling based methods use the theory of noise contrastive estimation guarantees are only asymptotic and not for downstream tasks. Conditional independence assumptions and redundancy assumptions on multiple views are used to analyze co-training not for downstream task
Summary
- Observations
- Forming the pretext tasks:
- Colorization: can be interpreted as \(p(X_1,X_2|Y)=p(X_1|Y)\times p(X_2|Y)\), aka \(X_1,X_2\) are independently conditioned on \(Y\)
- Inpainting: \(p(X_1,X_2|Y,Z)=p(X_1|Y,Z)\times p(X_2|Y,Z)\),aka the inpainted \(X_2\) is conditionally independent of \(X_2\) (the remainder) given \(Y,Z\).
- The only way to solve the pretext task is to first implicitly predict \(Y\) and then predict \(X_2\) from \(Y\)
- Forming the pretext tasks:
- Limitations:
- The underlying principles of self-supervised learning are still mysterious since it is a-priori unclear why predicting what we already know should help.
Goals
What conceptual connection between pretext and downstream tasks ensures good representations?
What is a good way to quantify this?
How?
Notations
| Symbol | Meaning |
|---|---|
| \(\mathbb{E}^L[Y|X]\) | the best linear predictor of \(Y\) given \(X\) |
| \(\Sigma_{XY|Z}\) | partial covariance matrix between \(X\) and \(Y\) given \(Z\) |
| \(X_1,X_2\) | the input variable and the target random variable for the pretext tasks |
| \(Y\) | label for the downstream task |
| \(P_{X_1X_2Y}\) | the joint distribution over \(\mathcal{X}_1 \times \mathcal{X}_2 \times \mathcal{Y}\) |
Idea
- Under approximate condition independence (CI) (quantified by the norm of a certain partial covariance matrix), show similar sample complexity improvements.
- Testify pretext task helps when CI is approximately satisfied in text domain.
- Demonstrate on a real-world image dataset that a pretext task-based linear model outperforms or is comparable to many baselines.
Formalize SSL with pretext task
It will be estimated by:
- approximation error:
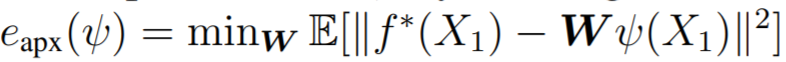, where \(f^*=\mathbb{E}[Y|X_1]\) is the optimal predictor for the task - estimation error:
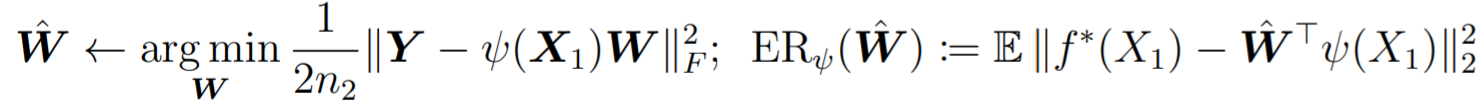, it's the difference between Predicting \(Y\) directly by \(X_1\) and Predicting by the representations from pretext task
Experiments
Conclusion
- This paper posits a mechanism based on conditional independence to formalize how solving certain pretext tasks can learn representations that provably decreases the sample complexity of downstream supervised tasks
- Quantify how approximate independence between the components of the pretext task (conditional on the label and latent variables) allows us to learn representations that can solve the downstream task with drastically reduced sample complexity by just training a linear layer on top of the learned representation.