Paper--Colorful Image Colorization

Paper Colorful Image Colorization

Code here

Why?

Previous work

Predicting colors in free way: taking the image’s \(L\) channel as input and its \(ab\) channels as the supervisory signal--> but tend to look desaturated, one explanation is using loss functions that encourage conservative predictions

• Non-parametric methods: given an input grayscale image, first define one or more color reference images. Then, transfer colors onto the input image from analogous regions of the reference image(s).

• Parametric methods: learn prediction functions from large datasets of color images at training time, posing the problem as either regression onto continuous color space or classification of quantized color values. --> Work in this paper is also classification task.

• Concurrent work on colorization

  Paper	loss	CNNs	Dataset
  Larsson et al.	un-rebalanced classification loss	hypercolumns on a VGG	ImageNet
  Iizuka et al.	regression loss	two-stream architecture in which fuse global and local features	Places
  This paper	classification loss, with rebalanced rare classes,	a single-stream, VGG-styled network with added depth and dilated convolutions	ImageNet

Summary

• Observations
  • Even in gray images, the semantics of the scene and its surface texture provide ample cues for many regions in each image
  • Color prediction is inherently multimodal --> sparks for a loss tailored to their work
• Limitations:
  • Loss only cares Euclidean distance: If an object can take on a set of distinct ab values, the optimal solution to the Euclidean loss will be the mean of the set. In color prediction, this averaging effect favors grayish, desaturated results. Additionally, if the set of plausible colorizations is non-convex, the solution will in fact be out of the set, giving implausible results.

Goals

Design colorization based pretext task to get a good image semantic representations: produce a plausible colorization that could potentially fool a human observer

How?

Idea

• Produce vibrant colorization: Predict a distribution of possible colors for each pixel. Then, re-weight the loss at training time to emphasize rare colors. This encourages the model to exploit the full diversity of the large-scale data on which it is trained. Lastly, produce a final colorization by taking the annealed mean of the distribution.
• Evaluate synthesized images: set up a “colorization Turing test”.

Data Preparation

• Quantize the \(ab\) output space into bins with grid size \(10\) and keep the \(Q = 313\) values which are in-gamut. Then this is the label \(Z\) of each pixel. Formally, denote the raw label as \(Y\), then \(Z = H^{−1}_{gt} (Y)\), which converts ground truth color \(Y\) to vector \(Z\).

Implementation

• Model

  

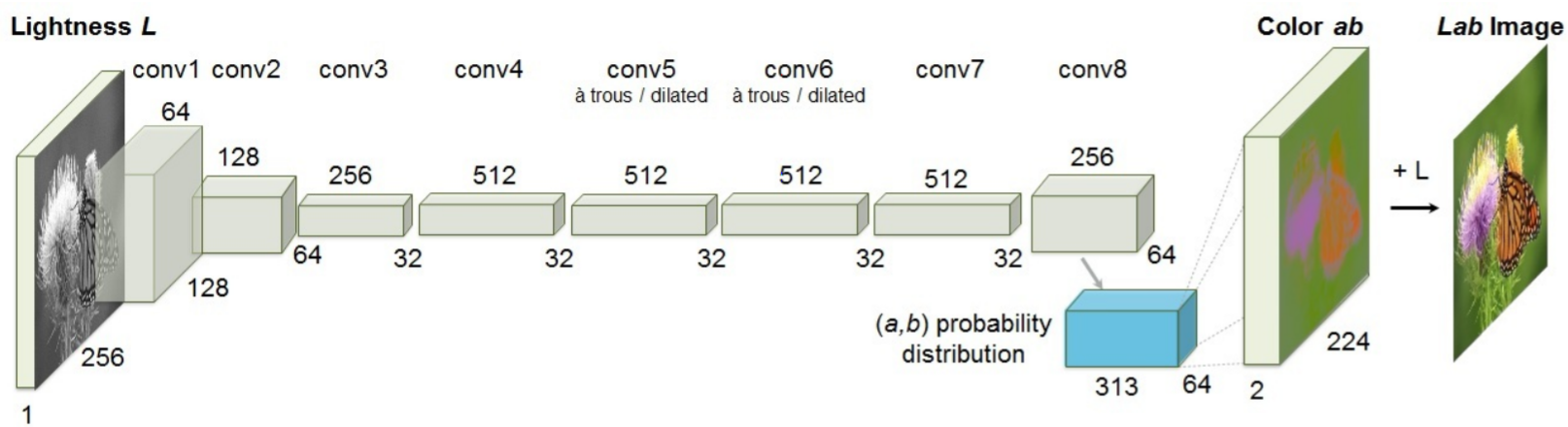
• Loss function

  

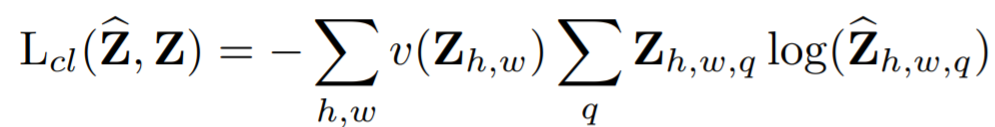
  where \(v(·)\) is a weighting term that can be used to re-balance the loss based on color-class rarity.

  • Re-balancing

    The distribution of \(ab\) values in natural images is strongly biased towards values with low \(ab\) values.

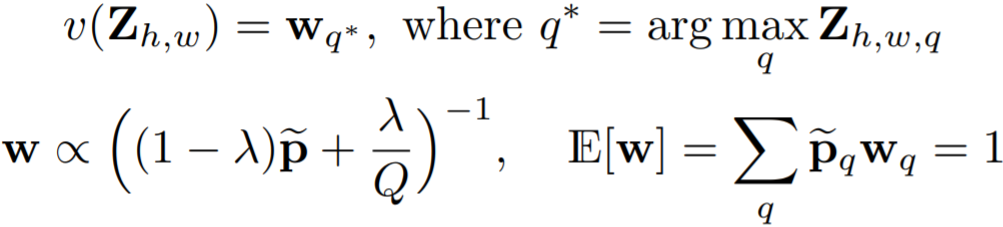    , where \(\tilde{p}\) the empirical probability of colors in the quantized ab space \(p\in \Delta Q\) from the full ImageNet training set and smooth the distribution with a Gaussian kernel \(G_{\sigma}\). \(\lambda=\frac{1}{2}, \sigma=5\) worked well.

• Inferring point estimates

  map probability distribution \(\hat{Z}\) to color values \(\hat{Y}\) with function \(\hat{Y} = H(\hat{Z})\)

They interpolate by re-adjusting the temperature \(T\) of the softmax distribution, and taking the mean of the result. Lowering the temperature \(T\) produces a more strongly peaked distribution, and setting \(T\rightarrow 0\) results in a 1-hot encoding at the distribution mode. They find that \(T=0.38\) captures the vibrancy of the mode while maintaining the spatial coherence of the mean.

Experiments

• Dataset: ImageNet
• Base models

Model Name	Loss	Train
Ours(full)	classification loss	from scratch with kmeans initialization, ADAM solver for about 450K iterations. \(\beta_1 = .9, \beta_2 = .99\), and weight decay = \(10^{−3}\) . Initial learning rate was \(3 × 10^{−5}\) and dropped to \(10^{−5}\) and \(3 × 10^{−6}\) when loss plateaued, at 200k and 375k iterations, respectively.
Ours(class)	classification loss withou rebalancing (\(\lambda=1\))	similar training protocol as Ours(full)
Ours(L2)	L2 regression loss	same training protocol
Ours(L2,ft)	L2 regression loss	fine tuned from our full classification with rebalancing network
Larsson et al.		CNN method
Dahl	L2 regression loss	a Laplacian pyramid on VGG features
Gray	--	every pixel is gray, with \((a, b) = 0\)
Random	--	Copies the colors from a random image from the training set

Colorization quality

• AMT: participants confirm their results. They argue that their work produce a more prototypical appearance for those are poorly white balanced
• Semantic interpretability (VGG classification): Are the results realistic enough colorizations to be interpretable to an off-the-shelf object classifier? They check it by by feeding their fake colorized images to a VGG network that was trained to predict ImageNet classes from real color photos.
  • The result is \(3.4\%\) lower than Larsson's.
  • Without any additional training or fine-tuning, one can improve performance on grayscale image classification, simply by colorizing images with our algorithm and passing them to an off-the-shelf classifier.
• Raw accuracy (AuC):
  • L2 metric can achieve accurate colorizations, but has difficulty in optimization from scratch
  • class-rebalancing in the training objective achieved its desired effect
• Compared with others
  • LEARCH: On SUN dataset, authors have \(17.2\%\) on AMT task while LEARCH has \(9.8\%\)

Cross-channel encoding as SSL Feature learning

• Datasets: ImageNet, PASCAL (fine tuned after training on ImageNet)
• Backbone: AlexNet
• Settings
  • ImageNet: fixing the extractor and retrain the classifier (softmax layer) by labels
  • PASCAL: : (1) keeping the input grayscale by disregarding color information (Ours (gray)) and (2) modifying conv1 to receive a full 3-channel \(Lab\) input, initializing the weights on the \(ab\) channels to be zero (Ours (color)).
• Summary
  • For ImageNet, there is a \(6\%\) performance gap between color and grayscale inputs. Except for the 1st layer, representations from other deeper layers catch and outperform most methods, indicating that solving the colorization task encourages representations that linearly separate semantic classes in the trained data distribution
  • On PASCAL, when conv1 is frozen, the network is effectively only able to interpret grayscale images.

The properties of network

• Is it exploiting low-level cues?

  Given a grayscale Macbeth color chart as input, it was unable to recover its colors. On the other hand, given two recognizable vegetables that are roughly isoluminant, the system is able to recover their color.

• Does it learn multimodal color distributions ?

  Take effective dilation ( the spacing at which consecutive elements of the convolutional kernel are evaluated, relative to the input pixels, and is computed by the product of the accumulated stride and the layer dilation) as the measurement. Through each convolutional block from conv1 to conv5, the effective dilation of the convolutional kernel is increased. From conv6 to conv8, the effective dilation is decreased

Conclusion

• Designing an appropriate objective function that handles the multimodal uncertainty of the colorization problem and captures a wide diversity of colors
• Introducing a novel framework for testing colorization algorithms, potentially applicable to other image synthesis tasks
• Setting a new high-water mark on the task by training on a million color photos.
• Introduce the colorization task as a competitive and straightforward method for self-supervised representation learning, achieving state-of-the-art results on several benchmarks.