Paper--Discriminative Unsupervised Feature Learning with Exemplar Convolutional Neural Networks

2021-01-06

Why?

Supervised : labeled data with a specific CNN
- directly penalizing the derivative of the output with respect to the magnitude of the transformations, but will be sensitive to the magnitude of the applied transformation.
Unsupervised: learning invariant representations
- Directly modeling the input distribution and are hard for jointly training multiple layers of a CNN
  - autoencoders: denoising auto encoders, say reconstruct data from randomly perturbed input samples; or learn representations from videos by enforcing a temporal slowness constraint on the feature representation learned by a linear autoencoder.
  - invariant to local transformations
- most aims at regularization of the latent representation
Semi-supervised
- Regularization supervised algorithms by unlabeled data: self-training, entropy regularization

Observations
- the features learned by one network often generalize to new datasets
- a network can be adapted to a new task by replacing the loss function and possibly the last few layers of the network and fine-tuning it to the new problem
Limitations:
- the need for huge labeled datasets to be used for the initial supervised training
- the transfer becomes less efficient the more the new task differs from the original training task

a more general extractor using unlabeled data. The extractor should satisfy two requirements:

there must be at least one feature that is similar for images of the same category $y$ (invariance);
there must be at least one feature that is sufficiently different for images of different categories (ability to discriminate)

Do random selected transformation (from a predefined family of transformations) for sampled patches (regions containing considerable gradients so that sample a patch with probability proportional to mean squared gradient magnitude within the patch )
The family of transformations
- translation
- scaling
- rotation
- contrast: PCA and HSV
- color: works on HSV space
- blur etc.
Before feeding into model, do normalization (subtract the mean of each pixel over the whole resulting dataset)
Labeling: all transformed patches from the same seed patch are labeled by the same index

Loss function :
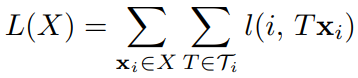
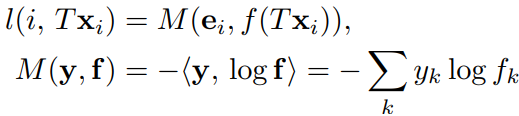
- After transformations, the loss for a whole class (augmented by the same seed patch ) can be taken as
  
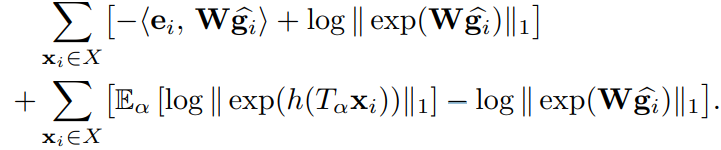  , notice the 2nd and the 4th can be canceled.
  - The 1st term: enforces correct classification of the average representation $\mathbb{E}_\alpha[g(T_\alpha x_i)]$ for a given input sample
  - The 2nd term: a regularizer enforcing all $ h(T_x_i)$ to be close to their average value, i.e., the feature representation is sought to be approximately invariant to the transformations $ T_$, note the convergence to global minimum is listed at appendix.
Why does it works?
- Previous works mostly focus on modeling the input distribution $p(x)$, based on the assumption that a good model of $p(x)$ contains information about the category distribution $p(y|x)$. Therefore, to get the invariance, one will do regularization of the latent representation and obtain representation by reconstruction .
- Their work does not directly model the input distribution $p(x)$ but learns a representation that discriminates between input samples. They argue that this allows more DOF to model the desired variability of a sample and avoid task-unnecessary reconstruction.
- However, their work will fail on color-relied task

Datasets: STL-10, CIFAR-10, Caltech-101 and Caltech-256. report mean and standard deviation

Datasets	Resizing	Train	Test
STL-10	64c5-64c5-128f	10 pre-defined folds of the training data	fixed test set
CIFAR-10	resize from $32\times 32$ to $64\times 64$	1. whole training set 2. 10 random selections of 400 training samples per class	1. results on CIFAR-10 2. average results on 10 sets.
Caltech-101	to $150\times 150$	30 random samples per class	not more than 50 samples per class
Caltech-256	$256\times 256$	randomly selected 30 samples per class	those except for training

backbones of network

Network	Structure	Training
small	64c5-64c5-128f	1.5 days, SGD with fixed momentum of 0.9
medium	64c5-128c5-256c5-512f	4 days, SGD with fixed momentum of 0.9
large	92c5-256c5-512c5-1024f	9 days, SGD with fixed momentum of 0.9

Training: learning rate starts at 0.01， then when there was no improvement in validation error, decreased the learning rate by a factor of 3. All networks are trained on one Titan
Test features: one-vs-all linear SVM.
Summary
- with increasing feature vector dimensionality and number of labeled samples, training an SVM becomes less dependent on the quality of the features
- Relation of the number of surrogate classes : sampling too many, too similar images for training can even decrease the performance of the learned features. ( the discriminative loss is no longer reasonable with too many similar surrogate classes.) --> fix: e.g. clustering the output features then do augmentation for clusters and feed these augmented classes as surrogate data
- Relation of the number of samples per surrogate class : around 100 samples is sufficient
- Relation of types of transformations : each time remove a group of transformations and check how the performance is decreased , e.g. scaling, rotation etc. Translations, color variations and contrast variations are significantly more important. For the matching task, using blur as an additional transformation improves the performance.
- Relation of Influence of the dataset : the learned features generalize well to other datasets
- Relation of Influence of the Network Architecture on Classification Performance: Classification accuracy generally improves with the network size

Task: Matching of interest points
Datasets: by Mikolajczyk et al., augmented by applying 6 different types of transformations with varying strengths to 16 base images from Flickr. In addition to the transformations used before, also change the lighting and blur .
Backbones: 64c7s2-128c5-256c5-512f, named as Exemplar-CNN-blur
Training: use unlabeled images from Flickr for training
Test and measurements: prediction is $TP$ if $IOU\ge 0.5$. Compared with SIFT and Alexnet
Summary
- Optimum patch size (or layer in CNNs): SIFT is based on normalized finite differences, and thus very robust to blurred edges caused by interpolation. In contrast, for the networks, especially for their lower layers, there is an optimal patch size. They argue that features from higher layers have access to larger receptive fields and, thus, can again benefit from larger patch sizes.
- A loss function that focuses on the invariance properties (rather than class-specific features) required for descriptor matching yields better results.
- Features obtained with the unsupervised training procedure outperform the features from AlexNet on both datasets

Pretty good on tasks: object classification , descriptor matching
emphasizes the value of data augmentation in general and suggests the use of more diverse transformations.